Electrostatics: Energy from a charge distribution

[WWCY]

Homework Statement

[/B]
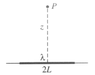
For a straight wire of length 2L carrying a uniform charge density $\lambda$, find
1) potential a distance z above the centre
2) electric field E at that point,
3) energy of this charge distribution

Homework Equations

The Attempt at a Solution

1) and 2) I can do, and their expressions are
$$V(z) = 2k_e\lambda \ln{\frac{L + \sqrt{l^2 + z^2}}{z}}$$
$$\vec{E} = \frac{2k_e \lambda L}{z\sqrt{z^2 + L^2}} \hat{k}$$

3) however, I have trouble with. Here's what I tried thus far.

I know that the energy needed to construct some line of charge is given by the expression
$$W = \frac{1}{2} \int \lambda V dl$$
where $V$ represents the potential associated with some point on the line of charge.

This is where I don't know how to continue. How does one find the potential such a point?

I tried
$$V(x) = k\lambda \int_{-L}^{L} \frac{1}{|x - x'|} dx'$$
where $x$ represents some point on the line charge, and $x'$ represents points on that line I'm integrating over. This however, seems to diverge.

Assistance is greatly appreciated!

 

[WWCY]

Could anybody take the time to assist? Many thanks!

 

[rude man]

I've been looking at this a bit; got the same E_z you did but that can't be right since obviously E_z(z=0) = 0.

As a parallel, the E field just above a finite conductive plate = σ/ε₀, not infinity. Can't see why a wire should be different.

I will look at this some more tomorrow (VERY late here!) And hopefully other help is on its way ...

 

[WWCY]

I've been looking at this a bit; got the same E_z you did but that can't be right since obviously E_z(z=0) = 0.

As a parallel, the E field just above a finite conductive plate = σ/ε₀, not infinity. Can't see why a wire should be different.

I will look at this some more tomorrow (VERY late here!) And hopefully other help is on its way ...

Thanks a lot for your time @rude man , appreciate it!

 

[rude man]

Thanks a lot for your time @rude man , appreciate it!

OK, here's my (I think) final take on this:
The wire has to have finite radius, otherwise you have infinite surface charge density which we don't allow. So you need to bring the radius into the picture. Call the radius a.

Then the potential of the wire is just 2kLλ/a. Now, as you accumulate charge to build up the wire to its full charge from zero, you can readily compute the work needed to do that by integrating over the charge accumulated from zero to 2λL.

 

[haruspex]

Then the potential of the wire is just 2kLλ/a

Isn't that for an infinite wire?

There are some difficulties with the question.

A wire is a conductor. A uniform charge would mean a non-uniform potential, therefore the charge would not be uniform. It would spread out towards the ends. So I guess they mean an insulator.

The theoretical potential of an infinitely thin wire would, as found, be infinite, yet the radius is not given.

 

[rude man]

Isn't that for an infinite wire?

No. Note the "L" in the potential expression. BUT - I am treating the wire as a point source which is of course not exact. I am at a loss as how to compute the actual potential of a finite-length wire of finite radius. Any ideas? I don't think it's infinite as for the case of (1) a wire of infinite length and (2) a wire of finite length and zero diameter.

A wire is a conductor. A uniform charge would mean a non-uniform potential, therefore the charge would not be uniform. It would spread out towards the ends. So I guess they mean an insulator.

. The wire is a conductor, therefore it is an equipotential. The charge distribution by itself does not seem to me to be material here.

ADDENDUM: the potential for an infinite wire of finite radius would be infinite.

Since the wire radius is not specified I assume they mean zero radius which means the required energy is infinite.

 

[haruspex]

No.

You are right, it isn't that either.
The potential for a finite uniform line of charge is as given in post #1, setting z=a.

 

[haruspex]

The wire is a conductor, therefore it is an equipotential. The charge distribution by itself does not seem to me to be material here.

One of the statements is false. Either it is not a wire or it is not a uniform charge distribution.
If we take it as a non-uniform distribution then the calculations of potential and field at P are invalid.

 

[rude man]

You are right, it isn't that either.
The potential for a finite uniform line of charge is as given in post #1, setting z=a.

EDIT: Hey, good point, so now we can write V(q) = (2kq/L) ln{(L+ √(L²+a²))/a}
then total energy required U(Q) = ∫V dq with limits q = 0 and Q, giving
U = U(Q) = k(Q^2//2)/L ln{(L+ √(L²+a²)/a} or
U = kλ²L ln{(L+ √(L²+a²)/a} since Q = 2Lλ.

 

[rude man]

One of the statements is false. Either it is not a wire or it is not a uniform charge distribution.
If we take it as a non-uniform distribution then the calculations of potential and field at P are invalid.

Well I think the charge distribution is pretty close to uniform even for a conducting wire. Perhaps the bunching of charge at the ends that you mention is negligible.

 

[haruspex]

Well I think the charge distribution is pretty close to uniform even for a conducting wire. Perhaps the bunching of charge at the ends that you mention is negligible.

It depends how you model the wire. As a cylinder, there is strong bunching near the ends, but relatively flat in the middle. As a narrow ellipsoid, the density is effectively uniform.
See e.g. https://www.colorado.edu/physics/phys3320/phys3320_sp12/AJPPapers/AJP_E&MPapers_030612/Griffiths_ConductingNeedle.pdf.

 

[rude man]

It depends how you model the wire. As a cylinder, there is strong bunching near the ends, but relatively flat in the middle. As a narrow ellipsoid, the density is effectively uniform.
See e.g. https://www.colorado.edu/physics/phys3320/phys3320_sp12/AJPPapers/AJP_E&MPapers_030612/Griffiths_ConductingNeedle.pdf.

OK, so we approximated best we could?

 

[haruspex]

OK, so we approximated best we could?

Not sure. The cylindrical solutions all seem to be numeric approximations, and the precise behaviour near the ends is unclear. What we need to know is the fraction of the total charge in, say, the end 5%.
In the article, I see reference to a power of -1/3 wrt charge density. That might mean the cumulative charge near the ends is like Δ(x^2/3). I need to study it more.

 

[WWCY]

Thank you both for your help!

I actually went to talk to a tutor about this in school. He said that I should find the expression for E field for general points and integrate over all space using this equation in perhaps spherical coordinates.
$$W = \frac{\epsilon _0}{2} \int E^2 \ dv$$
Is this something that makes sense?

 

[kuruman]

Is this something that makes sense?

I have followed this thread since you originally posted, but I kept myself from weighing in until now. Your instructor's suggestion was my original thought, however I got hung up on the issue that has already been identified, namely that if the wire is a conductor it cannot have uniform linear charge density and if it has uniform linear charge density then it cannot be a conductor. Nevertheless, I went ahead and found expressions for the field using cylindrical coordinates assuming a uniform $\lambda$ as the problem specified. I got a rather complicated expression for the energy density and I backed away from integrating it. I'm not saying it cannot be done, but I think there is a more direct way to see where this goes.

Let's say the wire is conducting and initially uncharged. We want to know the total work done putting total charge $Q$ on it. We bring charges $dQ'$ from infinity, put them one by one on the conductor and let them go where they will. Since the work is path-independent, we choose the perpendicular bisector as the path. Along this path, the potential (however it is calculated) must be independent of $z$ by symmetry and can be written as $Q'f(r)$ (the potential scales with $Q'$) where $Q'$ is the existing total charge on the wire. The work done to bring $dQ'$ from infinity and place it on the conductor is $dW=VdQ'=Q'dQ'f(r)$. The total work is found by integrating, $W=\frac{1}{2}Q^2f(r)$. This can also be viewed at the energy stored in a wire capacitor of capacitance $C=f(r)^{-1}$. Recasting the problem in these terms underscores the issue of the charge density or, more specifically, how one finds $f(r)$ and under what assumptions. I suspect that if you embark on doing the energy density integral you will spend a lot of time only to find that the integral diverges if you take the lower limit at $r=0$.

 

[haruspex]

find the expression for E field for general points

And how does the tutor propose you do that?
Did the tutor comment on the contradiction between "wire" and uniform distribution, or the worse problem that the answer depends on the radius of the wire?

 

[kuruman]

Ah, but there's the rub. If they do move it is to a lower energy state. The work released by moving is lost. So this method will overestimate the potential energy.

I thought about that, but then I managed to convince myself that I should not worry about what happens after $dQ'$ is placed on the conductor. I see your point, but isn't it appropriate to consider the wire as part of a capacitor with the second conductor being infinity? Then the energy stored is $U=Q^2/(2C)$ and all one has to do is find the capacitance which, of course, involves finding the potential at the wire. Is the use of $U=Q^2/(2C)$ questionable?

 

[haruspex]

I thought about that, but then I managed to convince myself that I should not worry about what happens after $dQ'$ is placed on the conductor. I see your point, but isn't it appropriate to consider the wire as part of a capacitor with the second conductor being infinity? Then the energy stored is $U=Q^2/(2C)$ and all one has to do is find the capacitance which, of course, involves finding the potential at the wire. Is the use of $U=Q^2/(2C)$ questionable?

I later found my argument unconvincing and deleted it, but you beat me to it.

 

[rude man]

Let's say the wire is conducting and initially uncharged. We want to know the total work done putting total charge $Q$ on it. We bring charges $dQ'$ from infinity, put them one by one on the conductor and let them go where they will. Since the work is path-independent, we choose the perpendicular bisector as the path. Along this path, the potential (however it is calculated) must be independent of $z$ by symmetry and can be written as $Q'f(r)$ (the potential scales with $Q'$) where $Q'$ is the existing total charge on the wire.

?? The potential is obviously a function of z, did you mean to say that (refOP's post 1)? I got the same expression as that of the OP. And what is r?

The OP and I have computed W = ∫V dq also and have found it to be infinite since the potential and E field both approach infiinity as z → 0. But maybe that assumed a uniform charge distribution which I realize is not possible for a finite-length conducting wire.

 

[kuruman]

?? The potential is obviously a function of z, did you mean to say that (refOP's post 1)? I got the same expression as that of the OP. And what is r?

I mentioned in post #16 that I used cylindrical coordinates as the problem has azimuthal symmetry. I conventionally took the wire to be on the z-axis with its two ends at $z=\pm L$. Variable $r$ is the radial distance from the z-axis. My $r$ is OP's $z$. I am sorry for not making this clearer in my previous message.

 

[haruspex]

maybe that assumed a uniform charge distribution

Infinities will arise as the radius tends to zero, regardless of the presumed density distribution.

 

[rude man]

I mentioned in post #16 that I used cylindrical coordinates as the problem has azimuthal symmetry. I conventionally took the wire to be on the z-axis with its two ends at $z=\pm L$. Variable $r$ is the radial distance from the z-axis. My $r$ is OP's $z$. I am sorry for not making this clearer in my previous message.

Oh right, thanks.
Another thing I did was (using your coord. system) put a right circular cylinder of width dz at z=0 and radius r. By that I found the E field to go as 1/r and the potential of course as ln r. If this gausssian surface is legitimate (no net E flux thru the flat sides) then the only conclusion I get is that λ must be zero around z=0. If that is not the case then I don't see how one can avoid the conclusion that the answer is that it takes infinite energy. Would appreciate your thoughts if you're inclined. @haruspex, same to you if you're reading this.

 

[rude man]

Infinities will arise as the radius tends to zero, regardless of the presumed density distribution.

But see my post 23?

 

[kuruman]

If this gausssian surface is legitimate ...

It is not. In fact a standard E&M problem is finding the E-field on the z-axis at some distance z from one of the ends. The Gaussian surface argument allows one to find the E-field only for an infinite wire. See for example http://www.phys.uri.edu/gerhard/PHY204/tsl31.pdf for the calculation of the field on the z-axis. Also, don't forget that at distances r (in whatever direction) such that $r >> L$, the finite line of charge must reduce to the spherically symmetric monopole electric field, i.e. the line of charge looks like a point charge (see limiting case L << D in link). This will not happen if there is zero electric flux through the flat faces of the Gaussian cylinder.

 

[rude man]

@kuruman Thanks for the comment and the link. Not sure what help it would have been anyway.
But having looked at the link, on 2nd slide it gives dE_x = kλ/y_p*(sin θ2 − sin θ1 )
which = 0 at the bisector presumably all the way to y = infinity so how can there be net flux into the sides of my gaussian surface? Slide 3 seems to further confirm that the field at the bisector is perpendicular to the line..

I wonder if you placed my gaussian correctly? You refer to slide 1 which computes the field coaxially but I'm looking at the field perpendicular to the rod at the midpoint of same, not the parallel one. Your opening line "In fact a standard E&M problem is finding the E-field on the z-axis at some distance z from one of the ends" seems to suggest that.

In any case I'm not sure what would be accomplished to find the charge distribution to be zero at the midpoint. With the gaussian surface I get ε₀E(2πr)dz = λ dz or E = 0/0 at z=0.

Sorry about all the edits.

 

[WWCY]

I'm not sure that I have understood each and every one of your posts, but let me try and have a go.

The issue highlighted by @haruspex and @rude man was that a finitely long conducting wire cannot have uniform charge density due to bunching, and a line with uniform charge density can't be a wire.

However, if I'm not mistaken, most of such problems assume that the line is an insulator (at least from my textbooks).

@kuruman then suggests that I could view this line as part of a capacitor with the other conductor at infinity. But this means that this line must be a conductor, and cannot have uniform charge density. If it isn't a conductor, it cannot be part of a capacitor.

Am I on the right track?

Also, thank you all for helping out. I'll see what is mentioned about the problem during class.

 

[kuruman]

Am I on the right track?

Yes. See if your instructor will clarify the conductor/insulator issue.

 

[rude man]

[QUOTE="WWCY, post: 5936139, member: 608494"[/QUOTE]
I would summarize my view as follows:
1. A zero-diameter wire, which I assume is conducting (most wires are! ), requires infinite energy to charge. Both the potential and the E field approach infinity as you get close to the wire. As I pointed out, zero radius implies infinite charge density and therefore again infinite E field.
2. But, there's no such thing as a zero-radius wire.
3. Therefore, it's necessary to consider a finite-radius wire and the radius will figure in determining the required energy.
4. I don't see why there is an issue with having a non-uniform charge distribution. Every finite conducting item, when charged, has non-uniform charge distribution. Approximations are always made.
5. I have not found a way to determine either the potential or the E field just above the radius of a finite-radius, finite-length wire, and seemingly neither has anyone else. But it seems obvious that only a finite amount of energy is required to charge the wire. So there's an answer somewhere.
6. Challenge your instructor to find that energy, using integrated energy density times volume as he/she suggested!
Cheers!

 

[WWCY]

Hi all, thank you for your helpful comments. Here's what I managed to find out

1) The problem was a bit of a mistake, my instructor set it without a solution in mind.
2) It was an insulator.
3) The potential and energy does diverge, but the instructor didn't delve into the calculations.

Apologies if this was a bit of a fruitless discussion, and thanks again for helping me consider some ideas that I previously never did.