Thanks for all your replies and sorry for the delay with my response, but I had little time last week and wanted to make sure I consider all arguments as thoroughly as possible. I can actually see where those are coming from, but lastly I can't (yet) see them resolving the paradox due to the issues addressed below:
BruceW said:
The work-energy principle for a point-like mass is:
Work = \int_{t1}^{t2} \vec{F} \cdot \vec{v} dt
And in this case, it is zero, because the only significant mass is the one in the middle, which has zero velocity for all time.
But there is no mass in your equation. What it says is that if you move a certain point of a mechanical system against some force over a certain path (or with a certain velocity for a certain time in your formulation), then this will require a certain work i.e. energy. The emphasis is clearly on the point of application here i.e. the point of constraint in this case, and by assumption this moves.
BruceW said:
How are you defining "a path that changes the state of the system" ? If you mean something like "the path of the connection point of the rod with the rail", then I challenge the physical meaning to this. Why is such a thing physically meaningful? Why would you choose that path, and not any other arbitrary path? For example, you could choose the path of any other point on the rod, and you would get a different answer for your 'work done'.
Well, if you would do the work at any other point of the rod, you would change the constraint; effectively you would have then a rail with a smaller radius and a shorter rod. This would be part of the paradox.
A.T. said:
Fantasist said:
n order to neutralize the gravitational force tangential to the rail, it would take either friction or some obstacle ...
...or two radial forces at \theta\pm\phi which both have non-zero tangential components w.r.t to the radius at \theta.
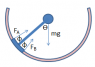
Only that the forces apply at \theta\pm\phi and not at \theta. Translating the vectors from the former to the latter obviously changes the scenario. Consider the following (slightly simpler) example
https://www.physicsforums.com/attachment.php?attachmentid=68144&stc=1&d=1396201366
you have a disk constrained at its center so that it can only rotate. There are two different radial forces ##F_A## and ##F_B## as indicated by the blue vectors. If you translate these vectors both to a common point and add them there, the sum will there have a tangential component ##F_T## (indicated in green), so the two forces should set the disk in rotation. Are you really suggesting the disk will be rotating in this scenario?
AlephZero said:
To get some sort of a solution to the problem, DaleSpam changed the problem, and made the "point" contact between the rod and the rail into two separated points.
That solution works mathematically, but only in the special case where the mass is at the center of the circle. But as a "real world" solution it is impractical, because as ##\phi \rightarrow 0## the two forces both ##\rightarrow \infty## (positive in opposite directions) but the difference between them stays finite and equal to ##mg## upwards.
Sorry, but for small ##\phi## I make this
##F_A - F_B = - mg/\phi*sin(\theta)##
##F_A + F_B = mg*cos(\theta)## (which is the radial component parallel to the arm)
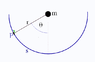
In any case, ##F_A## and ##F_B## are clearly defined as radial forces, so they can not produce any net force tangential to the rail that could compensate for the gravitational force (see my drawing above).
DaleSpam said:
Using Newton's 2nd law and noting that a=0 we write one expression for the component of the forces parallel to the arm:
## mg \cos(\theta) - F_A \cos(\phi) - F_B \cos(\phi)=0##
and another expression for the component of the forces perpendicular to the arm:
## mg \sin(\theta) + F_A \sin(\phi) - F_B \sin(\phi)=0##
What you have done here is to set up two equations of constraint, one for the net force along the arm
and one for the net force perpendicular to the arm (i.e. tangential to the rail). Effectively, this means you can't move anything anymore, and not surprisingly you won't be able to do any work then. The force components you thus get are just the forces of constraint in the material when you have locked everything in place, but this is not the scenario here.
The error you made here is to assume that the condition a=0 imposes a constraint on the motion perpendicular to the arm as well. It doesn't, as the mass can stay in the same place but still rotate.
Generally speaking, you should not bother about forces of constraint here at all. They may be of interest to material scientists, engineers or architects, but are irrelevant for the dynamical changes of a system.
DaleSpam said:
Now, as we move the attachment a small distance you want to consider the work done by the constraints (even though we know that constraints do no work, you want to prove it). So, since there are two constraints we get:
##dW=dW_F+dW_T##
where ##dW_F## is the work done by the net force and ##dW_T## is the work done by the net torque at the constraint. Then:
##dW_F=\mathbf{F}\cdot d\mathbf{s}=m\mathbf{g}\cdot d\mathbf{s} = -mg \sin(\theta) ds##
##dW_T=\tau \; d\theta = mg\; r \sin(\theta) d\theta##
and since ##r\;d\theta = ds## we have ##dW_T=-dW_F## so ##dW=0##.
Your basic mistake in the OP was that you analyzed only ##dW_F## and neglected ##dW_T##. That doesn't provide enough constraints to match what you were trying to do even in an abstract "let's not specify the mechanism" type analysis
I don't understand why you are bringing in the torque here. If you apply a force ##\mathbf{F}## to some point of a rigid body and move this point a distance ##d\mathbf{s}## in the process, then the work associated with this is ##\mathbf{F}\cdot d\mathbf{s}##, irrespectively of how much of this results in a translation of the center of mass and how much in a rotation due the torque associated with the force. If you say the total work done in the process is zero, then ##\mathbf{F}\cdot d\mathbf{s}## must be zero. But this contradicts your equation ##\mathbf{F}\cdot d\mathbf{s}=m\mathbf{g}\cdot d\mathbf{s} = -mg \sin(\theta) ds##.
Like I said already earlier, the important point here is that the work is done at the point of constraint, not directly at the mass.
 …
…