TimeRip496
- 249
- 5
Homework Statement
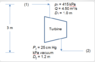
Water is supplied at 4.50 m3/s and 415 kPa (abs) to a hydraulic turbine through a 1.0-m inside diameter inlet pipe as indicated in the figure. The turbine discharge pipe has a 1.2-m inside diameter. The static pressure at section (2), 3 m below the turbine inlet, is 25 cm Hg vacuum. If the turbine develops 1.9 MW, determine the power lost between sections (1) and (2). (ANS:290kW)
Homework Equations
$${\displaystyle {{\frac {v_1^{2}}{2}}+gz_1+{\frac {p_1}{\rho }}=\frac {v_2^{2}}{2}}+gz_2+{\frac {p_2}{\rho }}+h_{shaft}+h_{lost}={\text{constant}}}$$
The Attempt at a Solution
To find the velocity,
$$v_1=4.50÷(0.5^2 \pi)=5.73 m/s $$
$$v_2=4.50÷(0.6^2 \pi)=3.98 m/s $$
Apply energy equation,
$$415(10^3) + 0.5\rho_w (5.73^2)+\rho_w g(3) = 1.9(10^6)÷4.5 +\frac{25}{76}(1.01*10^5)+0.5\rho_w (3.98^2)+P_{lost}÷4.5 $$ $$ P_{lost}=4.5(460846.45-463366.12)=-11338.515$$
However this is not possible as the power lost must be positive based on the above formulated steps. Besides the answer is not the same as the correct answer which is 290kW.