Energy Transfer Between Inertia Wheels

In summary, the conversation discusses a physics problem involving two inertia wheels on separate shafts connected by a clutch. The question is what the final rpm of both wheels will be after the clutch is engaged. The person is struggling to find a similar problem to use as an example and is looking for guidance on how to determine the final torque and rpm. The solution involves using conservation of angular momentum, assuming the bearings are in good condition.
  • #1
DrunkElk1601
1
0
TL;DR Summary
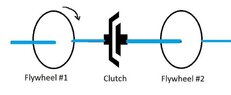
One flywheel is spinning and a 2nd flywheel is at rest. A clutch connects the shafts. What's the final rpm?
Been 20 years since college physics. I have a problem where there are basically two inertia wheels on separate shafts coupled by a clutch. One wheel is spinning and the other is at rest. The clutch engages and connects the shafts. What's the final rpm of both wheels? I'm struggling to find a similar problem to use an example. I know the radius, KE, moment of inertia, rpm, clutch engagement time, etc. but I'm not sure how to determine the final torque because it's not clear how to find the final rpm. If you would please describe the general approach or link a similar problem I'd appreciate it.
 

Attachments

  • flywheels and clutch problem.jpg
    flywheels and clutch problem.jpg
    17.2 KB · Views: 107
Physics news on Phys.org
  • #2
Conservation of angular momentum.
 
  • #3
If the bearings are good then you can use conservation of angular momentum
 

FAQ: Energy Transfer Between Inertia Wheels

What is energy transfer between inertia wheels?

Energy transfer between inertia wheels refers to the process of transferring energy from one inertia wheel to another. Inertia wheels are rotating disks that store kinetic energy and can transfer it to other objects or systems through physical contact or electromagnetic fields.

How does energy transfer occur between inertia wheels?

Energy transfer between inertia wheels occurs through physical contact or through electromagnetic fields. In physical contact, the inertia wheels must be connected in some way, such as through a shaft, for the energy to transfer. In electromagnetic fields, the wheels can transfer energy without physical contact, but must be in close proximity to each other.

What are the applications of energy transfer between inertia wheels?

Energy transfer between inertia wheels has various applications in different fields. In spacecrafts, it is used for attitude control and stabilization. In electric vehicles, it is used for regenerative braking to convert kinetic energy into electrical energy. It is also used in flywheels for energy storage and in gyroscopes for navigation systems.

Can energy transfer between inertia wheels be controlled?

Yes, energy transfer between inertia wheels can be controlled through various methods such as changing the speed or direction of rotation of the wheels, adjusting the physical contact between the wheels, or altering the strength of the electromagnetic fields. These controls can be used to regulate the amount and direction of energy transfer.

Are there any limitations to energy transfer between inertia wheels?

Yes, there are some limitations to energy transfer between inertia wheels. One limitation is the efficiency of the transfer, as some energy may be lost due to friction or other factors. Another limitation is the maximum amount of energy that can be transferred, which is dependent on the size and speed of the inertia wheels. Additionally, energy transfer between inertia wheels may not be suitable for all applications and may require additional components or systems for optimal performance.

Similar threads

I How does the mass of the wheels affect the car's acceleration?
Replies
15
Views
3K
Inertia of the drivetrain components of a 4x4 vehicle
Replies
15
Views
2K
Calculate RPM for Launching Ball by Flywheel
Replies
12
Views
1K
I How to transfer angular momentum between two flywheels?
Replies
8
Views
2K
B The physics of flywheel launchers (like tennis ball shooters)
2
Replies
60
Views
766
I How do we calculate the energy we used to do something?
Replies
10
Views
1K
I I'm calculating more energy out than I put in
4
Replies
138
Views
6K
I Is it possible to create linear acceleration using nothing but different moments of inertia beteen a wheel and axle?
Replies
5
Views
990
I Figuring out the torque required to rotate a dome
Replies
16
Views
2K
I Control Moment Gyro - MOI calculation & units of measure
Replies
12
Views
2K

Hot Threads

Recent Insights

Back
Top