yugeci
- 61
- 0
Homework Statement
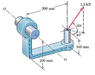
I have attached the diagram. The question says "Compute the Moment Mo of the 1.2kN force about the axis O-O.
Homework Equations
M = r x F
AB = OB - OA
Resolving forces, Fx = F cos Θ.. Fy = F sin Θ etc.
The Attempt at a Solution
Here are the axes I've made, using the Right Hand Rule:
OA = (-300, 0, 105)
OB = (0, 0, 200)
So AB = (300, 0, 95) .. this is the r vector.
For the F vector, Fz = 1.2 sin 60 = 1.04 kN
Fxy = 1.2 cos 60 = 0.6 kN
Fx = -0.6 cos 50 = -0.39 kN
Fy = 0.6 sin 50 = 0.46 kN
M = r x F (since we need the moment about the O-O axis, I'll just get the j component).
| 300 0 95 |
| -0.39 0.46 1.04 |
Solving gives M @ o-o as -349.05 Nm. However the answer is +327 Nm. What have I done wrong?