You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How Do You Solve Difficult Engineering Statics Problems?
- Thread starter ODU
- Start date
-
- Tags
- Engineering Statics
AI Thread Summary
To solve difficult Engineering Statics problems, it's essential to establish static equilibrium at key points, such as point A, to analyze forces and tensions. If a force acts directly at point A, determine the compression in the member by setting up equilibrium equations. If the force is at another point, identify the vertical component affecting the structure, using static equilibrium principles to trace forces in each member. Reviewing fundamental concepts and collaborating with peers or instructors can provide clarity and new insights. Persistence and seeking assistance are crucial for overcoming challenging engineering problems.
Physics news on Phys.org
Zaphodx57x
- 30
- 0
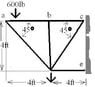
Is that force directly at point A? Is that a second force at the bottom?
If I remember correctly, you usually have to find the spot where only components of tension and force in one direction can be calculated. Like, if that force is directly at point A then set up a static equilibrium calculation at point a, where member ab has no compression or tension directly due to the force. That way the member ad(you don't have this point marked) must be compressed.
And 600lb = adsin(45), solve for ad making note of compression, then go back to point a and do a static equilibrium calculation for the horizontal components, now knowing ad, you can find ab.
If that force is at some random point along that member, then I think you can find the vertical component at c because it looks to me that c is the only thing holding that balcony up. The same principles of static equilibrium will allow you to trace out the forces in each member.
Hopefully all that I said helps and is correct.
If I remember correctly, you usually have to find the spot where only components of tension and force in one direction can be calculated. Like, if that force is directly at point A then set up a static equilibrium calculation at point a, where member ab has no compression or tension directly due to the force. That way the member ad(you don't have this point marked) must be compressed.
And 600lb = adsin(45), solve for ad making note of compression, then go back to point a and do a static equilibrium calculation for the horizontal components, now knowing ad, you can find ab.
If that force is at some random point along that member, then I think you can find the vertical component at c because it looks to me that c is the only thing holding that balcony up. The same principles of static equilibrium will allow you to trace out the forces in each member.
Hopefully all that I said helps and is correct.
wais
- 1,225
- 0
I understand that you are struggling with a difficult Engineering Statics problem and are seeking help. It can be frustrating when you are unable to solve a problem, especially when you have been working on it for days. However, it is important to remember that seeking help is a sign of strength and determination to overcome challenges.
I suggest reaching out to your professor or a teaching assistant for assistance. They are there to help and guide you through difficult concepts. You can also seek help from classmates or join a study group to work on the problem together. Sometimes, discussing the problem with others can provide new perspectives and help you approach it in a different way.
Additionally, make sure you have a good understanding of the fundamentals of Engineering Statics. Review your notes, textbook, and class materials to refresh your knowledge. Sometimes, going back to the basics can help you solve more complex problems.
Lastly, don't get discouraged. Engineering problems can be challenging, but with determination and persistence, you will be able to find a solution. Keep pushing through and don't be afraid to ask for help when you need it. Best of luck to you!
Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system
$$M(t) = M_{C} + m(t)$$
$$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$
$$P_i = Mv + u \, dm$$
$$P_f = (M + dm)(v + dv)$$
$$\Delta P = M \, dv + (v - u) \, dm$$
$$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$
$$F = u \frac{dm}{dt} = \rho A u^2$$
from conservation of momentum , the cannon recoils with the same force which it applies.
$$\quad \frac{dm}{dt}...
I was thinking using 2 purple mattress samples, and taping them together, I do want other ideas though, the main guidelines are;
Must have a volume LESS than 1600 cubic centimeters, and CAN'T exceed 25 cm in ANY direction.
Must be LESS than 1 kg.
NO parachutes.
NO glue or Tape can touch the egg.
MUST be able to take egg out in less than 1 minute.
Grade A large eggs will be used.
Similar threads
- Replies
- 11
- Views
- 3K
- Replies
- 9
- Views
- 2K
- Replies
- 16
- Views
- 3K
- Replies
- 1
- Views
- 2K
- Replies
- 8
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 5
- Views
- 2K
- Replies
- 8
- Views
- 852
- Replies
- 15
- Views
- 2K
- Replies
- 4
- Views
- 738
Hot Threads
-
Torque biomechanics
- Started by Naucus
- Replies: 6
- Introductory Physics Homework Help
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 11
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math