exi
- 85
- 0
Homework Statement
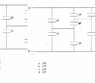
What is the equivalent capacitance for the following schematic?
Note that C1 is 11 µF, and C2 is 3 µF.
http://img511.imageshack.us/img511/8051/questionzi5.png
Homework Equations
C_{parallel} = C_1 + C_2 + C_3 + ... + C_n
\frac{1}{C_{series}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + ... + \frac{1}{C_n}
The Attempt at a Solution
I tried the following:
1: Considered the four right-hand caps to be in parallel and add them as above, yielding 47 µF, and:
2: Added that 47 µF cap in series with the remaining 5 µF and 3 µF caps like so:
C_{eq} = \frac{1}{\frac{1}{5} + \frac{1}{47} + \frac{1}{3}} = 1.8051 \mu F
But no go (and appropriately so, since the number seems a bit small). Where am I making a mistake?
Last edited by a moderator: