You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
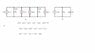
Equivalent Circuits: How Do (a) & (b) Compare?
- Thread starter Miike012
- Start date
AI Thread Summary
Circuits (a) and (b) are equivalent due to their parallel configuration, where the voltage remains constant across the upper and lower nodes. The current i0 is the sum of two currents flowing from high to low potential, but its flow is influenced by the fixed current sources and the voltage imposed by the ideal voltage source v(t). The analysis focuses on the current distributions through the resistors, as the voltage across them dictates the current flow according to Ohm's Law. Even if a large current source, such as i4(t), is introduced, it does not affect the current through the resistors because the voltage source v(t) controls the voltage across them. Ultimately, the current generated at the + terminal returns to the - terminal, with the voltage source adjusting to maintain its output voltage.
Physics news on Phys.org
UltrafastPED
Science Advisor
Gold Member
- 1,910
- 216
Note that this circuit is parallel, and hence we know that the voltage is the same all along the upper bus (or node if you prefer), and along the lower bus. They have specified that the upper node is +. Thus all of the interesting action is in the current distributions. Since the current sources have fixed currents ... we are most interested in the currents flowing through the two resistors.
The first equation is KCL with all of the currents originating at the upper node.
The second equation is a rearrangement, putting the currents that pass through the resistors on one side, and the current sources on the other.
The third equation is a definition which combines the current sources.
The drawing is a simplified circuit - all of the current sources have been combined - and the voltage difference between the nodes has been noted in a different place. Currents i2 and i5 have not been labeled, but they belong with the two resistors.Yes: "i0 is the sum of two currents" ... and you can see that the arrows for i2 and i5 should go from top to bottom "from high to low potential (flow of positive charge)".
"So why does i0 not flow from high to low pot?" ... the current generated at the + terminal must all return to the - terminal if there is no charge storage: it flows from the generator to the + node, then down through the two resistors (you need to put the current flow arrows on the diagram), to the lower node, and then returns to the - terminal of the current generator. "So why does i0 not flow from high to low pot?" - it does - and then returns to the generator.
The first equation is KCL with all of the currents originating at the upper node.
The second equation is a rearrangement, putting the currents that pass through the resistors on one side, and the current sources on the other.
The third equation is a definition which combines the current sources.
The drawing is a simplified circuit - all of the current sources have been combined - and the voltage difference between the nodes has been noted in a different place. Currents i2 and i5 have not been labeled, but they belong with the two resistors.Yes: "i0 is the sum of two currents" ... and you can see that the arrows for i2 and i5 should go from top to bottom "from high to low potential (flow of positive charge)".
"So why does i0 not flow from high to low pot?" ... the current generated at the + terminal must all return to the - terminal if there is no charge storage: it flows from the generator to the + node, then down through the two resistors (you need to put the current flow arrows on the diagram), to the lower node, and then returns to the - terminal of the current generator. "So why does i0 not flow from high to low pot?" - it does - and then returns to the generator.
CWatters
Science Advisor
Homework Helper
Gold Member
- 10,546
- 2,324
The voltage across the resistors is determined by v(t) because an ideal voltage source will impose it's voltage on anything.
If you have something that controls the voltage across a resistor the current through it will also be controlled. See ohms law.
If the voltage and current through the resistors is controlled by v(t) then I3(t) and I4(t) and i6(t) have no effect on the voltage or current through the resistors.
If you are only interested in the voltage and current through the resistors you can therefore model the circuit as either a single voltage source or as a single current source that performs the same function as V(t). They have chosen a current source io(t).
Lets say i4(t) was a massive current source of 1,000,0000 amps. That still wouldn't effect the current through the resistors because v(t) controls the voltage across them. So where does all the current go? The answer is that most of it will go through the voltage source v(t). An ideal voltage source _will_ source or sink whatever current is necessary to maintain it's output voltage.
If you have something that controls the voltage across a resistor the current through it will also be controlled. See ohms law.
If the voltage and current through the resistors is controlled by v(t) then I3(t) and I4(t) and i6(t) have no effect on the voltage or current through the resistors.
If you are only interested in the voltage and current through the resistors you can therefore model the circuit as either a single voltage source or as a single current source that performs the same function as V(t). They have chosen a current source io(t).
Lets say i4(t) was a massive current source of 1,000,0000 amps. That still wouldn't effect the current through the resistors because v(t) controls the voltage across them. So where does all the current go? The answer is that most of it will go through the voltage source v(t). An ideal voltage source _will_ source or sink whatever current is necessary to maintain it's output voltage.
Last edited:
Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system
$$M(t) = M_{C} + m(t)$$
$$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$
$$P_i = Mv + u \, dm$$
$$P_f = (M + dm)(v + dv)$$
$$\Delta P = M \, dv + (v - u) \, dm$$
$$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$
$$F = u \frac{dm}{dt} = \rho A u^2$$
from conservation of momentum , the cannon recoils with the same force which it applies.
$$\quad \frac{dm}{dt}...
I was thinking using 2 purple mattress samples, and taping them together, I do want other ideas though, the main guidelines are;
Must have a volume LESS than 1600 cubic centimeters, and CAN'T exceed 25 cm in ANY direction.
Must be LESS than 1 kg.
NO parachutes.
NO glue or Tape can touch the egg.
MUST be able to take egg out in less than 1 minute.
Grade A large eggs will be used.
Similar threads
- Replies
- 2
- Views
- 2K
- Replies
- 10
- Views
- 372
- Replies
- 3
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 10
- Views
- 2K
- Replies
- 4
- Views
- 1K
- Replies
- 3
- Views
- 1K
- Replies
- 31
- Views
- 4K
- Replies
- 4
- Views
- 2K
- Replies
- 1
- Views
- 1K
Hot Threads
-
Torque biomechanics
- Started by Naucus
- Replies: 6
- Introductory Physics Homework Help
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 6
- Quantum Physics
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 10
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math