cjames9001
- 5
- 0
Homework Statement
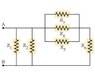
Find the equivalent resistance between points A and B shown in the figure . Consider R1 = 4.8 Ohms, R2 = 2.5 Ohms, R3 = 3.7 Ohms, R4 = 4.4 Ohms, R5 = 4.1 Ohms, and R6 = 6.4 Ohms.
Homework Equations
The Attempt at a Solution
I got 9.33 by adding resistors 3,4,5 in parallel [1/(1/R3+1/R4+1/R5)] and added that to R6 which is in series with the equivalent of 3,4,5 and I added 1,2 In parallel [1/(1/R1+1/R2)]. My question is that obviously I am not combing the right resistors as parallel or series, can someone help me on this? I have also tried the equivalent of 3,4,5 in parallel and adding that to the equivalent of 1,2,6 in parallel which I believe is about 2.66 anyways I've tried a few other combinations as well and cannot seem to figure out which ones I am supposedto add in parallel and which ones to add in series
Homework Statement
Homework Equations
The Attempt at a Solution
Attachments
Last edited by a moderator: