Equivalent Resistance Homework: Help Needed!

[yecko]

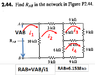
Homework Statement

Homework Equations

parallel(two shared nodes in two sides), series resistor(one shared node between 2 resistors)

The Attempt at a Solution

I can't identify the circuit to be parallel or series in order to get the equivalent resistance.
how should I finish the question?

( correction: answer=6kΩ)
as i will have exam few hours later... please help! thanks!

 

[Henryk]

It's against my religion to offer full solution but I can give you a hint:
If you look how the 12 $k\Omega$ is connected, you notice that there is no voltage across it, so, no current. Just remove it from the circuit and continue.

 

[yecko]

If you look how the 12 kΩkΩk\Omega is connected, you notice that there is no voltage across it,

you should be right, when I shorted the 12 kΩ, i can get the correct answer of 6kΩ
but why no voltage across it?

 

[yecko]

what if this kind of asymmetric circuit?

 

[jaus tail]

Convert the upper triangle from delta to star.

 

[yecko]

Convert the upper triangle from delta to star.

what do you mean by "delta" and "star"?
(i have never learned wheatstone bridge...)

 

[jaus tail]

Have you been taught star-delta resistance transformation?
Or only Rseries and Rparallel?

 

[yecko]

Only R series and parallel...

 

[gneill]

Only R series and parallel...

If you are unfamiliar with the Δ-Y transformations (It would be worth your while to look it up!), then an alternative is to apply a voltage source across AB and solve the circuit for the current that the source produces. Ohm's law will then tell you the effective load resistance.

 

[jaus tail]

If you are unfamiliar with the Δ-Y transformations (It would be worth your while to look it up!), then an alternative is to apply a voltage source across AB and solve the circuit for the current that the source produces. Ohm's law will then tell you the effective load resistance.

Even if a voltage source is applied, wouldn't star-delta transformation be needed. I don't think there is any other way to find the currents.
Nodal analysis?

 

[Babadag]

 

[mpresic2]

the four 9 ohm resistors (two in each series) can be replaced judiciously by two six ohm resistors and two 12 ohm resistors in series with two six ohm resistors. Then you have a symmetric circuit around the middle 12 ohm resistor. Because of symmetry, there is no reason to expect a different potential at either end of the middle 12 ohm resistor. Clever problem eh.?

 

[The Electrician]

Babadag, there's no need to derive a mesh solution. Simple reduction by various parallel and series combinations gives 6 ohms.

 

[Babadag]

You are right. My mistake. The result is 6 indeed.

 

[Henryk]

I actually said 'remove it'.

but why no voltage across it?

If you look at the circuit, the left side of the 12 $k\Omega$ resistor is connected to the right sides of both 3 $k\Omega$ via the same resistances, hence it's voltage is an average of the corresponding nodes voltages. The same is true for the right side of that resistor.
And the final proof: you shorted it and got the correct answer. Now remove it and redo the calculations, you'll get exactly the same answer.

what do you mean by "delta" and "star"?
(i have never learned wheatstone bridge...)

Do you know the loop current method? you can use that too.

 

[gneill]

Even if a voltage source is applied, wouldn't star-delta transformation be needed. I don't think there is any other way to find the currents.
Nodal analysis?

No, you can avoid star-delta if you apply mesh or nodal analysis, or even "raw" KVL and KCL equations with branch currents.

 

[jaus tail]

the four 9 ohm resistors (two in each series) can be replaced judiciously by two six ohm resistors and two 12 ohm resistors in series with two six ohm resistors. Then you have a symmetric circuit around the middle 12 ohm resistor. Because of symmetry, there is no reason to expect a different potential at either end of the middle 12 ohm resistor. Clever problem eh.?

I'm struggling to understand this. Can you please post a picture of the configuration?

 

[NascentOxygen]

I'm struggling to understand this. Can you please post a picture of the configuration?

The 9kΩ resistors are arranged as a potential divider, setting their midpoint at (in this case) 50% of the potential across them all. The pair of 6kΩ resistors likewise form a similar potential divider ...