- #1
Frankenstein19
- 56
- 0
Homework Statement
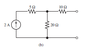
Find the Thévenin resistance for each of the circuits shown by zeroing the sources.
Homework Equations
The Attempt at a Solution
I replaced the current source with an open circuit and I'm left with a wye formation but I don't know how to calculate the equivalent resistance