Equivalent Resistance in partial parallel/series cicuit

[thatgirlyouknow]

Homework Statement

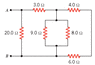
Find the equivalent resistance between points A and B in the drawing.

Homework Equations

Rseries = R1+R2+R3...
Rparallel: 1/Rp = 1/R1+1/R2+1/R3...

The Attempt at a Solution

Reducing it down:
1/8+1/9 = 1/R1 = 4.235
That's in parallel with 20, so:
1/20+1/4.235 = 3.495 ohms

3, 4, and 6 are in series:
3+4+6 = 13 ohms
Add that to the previous and you have 16.495 ohms, which is incorrect.

Is one parallel and I'm not adding it as such? Or should I combine differently?

Thanks so much!

 

[Doc Al]

Reducing it down:
1/8+1/9 = 1/R1 = 4.235

Good. R1 = 4.235 (not 1/R1).

That's in parallel with 20, so:

Nope. The 3 ohm resistor is in the way.

 

[thatgirlyouknow]

So then 20 and 3 are in series, right?
20+3=23 ohms

So now my drawing has:

23 ohms . 4 ohms

4.235 ohms

. 6 ohms

Would the 4 and 6 be considered series?

 

[Cynapse]

4+6 are in series
9+8 are in parallel
3 and 20 are not in series!

You need to do this step by step...

6+4 = 10
1/8 + 1/9 = 17/72
now you have

------3 -----------
--|--------|------|
-20------17/72--10
--|--------|------|
-------------------

Next you have 17/72 and 10 in parallel.

1/10+72/17 = 737/170

-- -- 3 -------
--|---------|
-20------737/170
--|---------|
--------------

Now the 3 and 737/170 are in series so just add them to get

-------------
--|---------|
-20-------1147/170
--|---------|
-------------

Now these are in parallel you can solve!

 

[thatgirlyouknow]

When you added for 17/72 and 10 in parallel, shouldn't it have been 1/4.235+1/10 = 1/R = 2.975?

so then with
------3--------
| |
20 2.975
| |
------------

So now which should I combine first?

 

[physixguru]

first take this and then you shall have the feel of the question much better..""

General rules for doing the reduction process include:

1. Two (or more) resistors with their heads directly connected together and their tails directly connected together are in parallel, and they can be reduced to one resistor using the equivalent resistance equation for resistors in parallel.

2. Two resistors connected together so that the tail of one is connected to the head of the next, with no other path for the current to take along the line connecting them, are in series and can be reduced to one equivalent resistor.

Finally, remember that for resistors in series, the current is the same for each resistor, and for resistors in parallel, the voltage is the same for each one