Espheric to cartesian coordinates

[Telemachus]

Homework Statement

Hi there. Well, I have the next exercise, which I've solved, but I don't know if the solution I got is the right one.

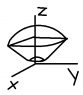
It says Given the next region on spheric coordinates find the expression for it in rectangular coordinates, and plot.

$$\phi\in{(0,\displaystyle\frac{\pi}{6}}),\rho\in{[1,2],\theta\in{(0,\displaystyle\frac{\pi}{2}})}$$

Well, In think it is a part of a cone, without a sphere of radius 1, with a sphere of radius 2 on the top.

Homework Equations

$$\begin{Bmatrix}{ x=\rho\cos\theta\sin\phi}\\y=\rho^2\sin\theta\sin\phi\\z=\rho\cos\phi \end{matrix}$$

The Attempt at a Solution

$$x^2+y^2=\rho^2\sin^2\phi(\cos^2\theta+\sin^2\theta)\Rightarrow{x^2+y^2=\rho\sin^2\phi}$$

$$z^2=\rho^2\cos^2\phi\Rightarrow{\rho^2=\displaystyle\frac{z^2}{\cos^\phi}}$$

$$x^2+y^2=z^2\displaystyle\frac{\sin^2\phi}{\cos^2\phi}\theta}\Rightarrow{x^2+y^2=z^2\tan^2\phi}\Rightarrow{x^2+y^2\leq{\displaystyle\frac{z^2}{3}}}$$

$$f(x,y)=\begin{Bmatrix}{ x^2+y^2\leq{\frac{z^2}{3}}\forall{}z\in{[\frac{\sqrt[ ]{3}}{2}},\sqrt[ ]{3}]}\\x^2+y^2+z^2\leq{4}\forall{z\in{(\sqrt[ ]{3},2]}}\\x^2+y^2+z^2\geq{1} \end{matrix},x>0,y>0$$

Is this right?

 

[gabbagabbahey]

$$x^2+y^2=\rho^2\sin^2\phi(\cos^2\theta+\sin^2\theta)\Rightarrow{x^2+y^2=\rho\sin^2\phi}$$

You dropped a superscript, you should have $x^2+y^2 =\rho^2\sin^2\phi$.

$$z^2=\rho^2\cos^2\phi\Rightarrow{\rho^2=\displaystyle\frac{z^2}{\cos^\phi}}$$

What if $\cos\phi = 0$?

$$x^2+y^2=z^2\displaystyle\frac{\sin^2\phi}{\cos^2\phi}\theta}\Rightarrow{x^2+y^2=z^2\tan^2\phi}\Rightarrow{x^2+y^2\leq{\displaystyle\frac{z^2}{3}}}$$

There's a much easier way to relate Cartesian coordinates to spherical coordinates, that is probably derived in your textbook/notes:

$$\rho = \sqrt{x^2+y^2+z^2}$$
$$\theta = \cos^{-1}\left(\frac{z}{\sqrt{x^2+y^2+z^2}}\right)$$
$$\phi = \tan^{-1}\left(\frac{y}{x}\right)$$

Your bounds on $r$, $\theta$ and $\phi$ each give you two inequalities (for a total of 6 inequalities) which you need to reduce/solve to find the region in closed.

For example, $\phi \in (0,\frac{\pi}{6})$ tells you that $0 < \tan^{-1}\left(\frac{y}{x}\right) < \frac{\pi}{6}$, or, taking the tangent of each side of this inequality (actually 2 inequalities combined into one expression),

$$0 < \frac{y}{x} < \frac{1}{\sqrt{3}}$$

You've correctly found that $x^2+y^2 < \frac{z^2}{3}$, but that only makes use of one of the 6 inequailties you have. You need to use them all to get the correct region.

$$f(x,y)=\begin{Bmatrix}{ x^2+y^2\leq{\frac{z^2}{3}}\forall{}z\in{[\frac{\sqrt[ ]{3}}{2}},\sqrt[ ]{3}]}\\x^2+y^2+z^2\leq{4}\forall{z\in{(\sqrt[ ]{3},2]}}\\x^2+y^2+z^2\geq{1} \end{matrix},x>0,y>0$$

Is this right?

Here I'm not sure what you're trying to say...there is no f(x,y) in this case, you are simply being asked to find a reduced set of inequalities for $x$, $y$ and $z$ that describe the region...Is there another part of the problem that involves some function f(x,y)?

 

[Telemachus]

No, I've called f(x,y) to the region.

Im calling $$\phi,\theta,\rho$$ this way:

[PLAIN]http://www.math.montana.edu/frankw/ccp/multiworld/multipleIVP/spherical/convert3d.gif

And $$\rho\geq{0}$$

You dropped a superscript, you should have $x^2+y^2 =\rho^2\sin^2\phi$.

Sorry, it was a typo, I'll correct it.

[tex]What if $$\cos\phi = 0$$?

Then $$z=\rho$$

Thanks for your answer. I've found a set of inequalities (thats the last set of equations I've posted), I'll try to make a graph of "what I see".

 

[gabbagabbahey]

No, I've called f(x,y) to the region.

That doesn't make any sense to me. In Cartesian coordinates, your region should be described by a set of inequalities for x,y and z (the same way it is desribed by a set of inequailties for $\rho$, $\theta$ and $\phi$ when working in spherical coordinates), not by some function f(x,y).

For example, if I wanted to describe the region the is bounded by the planes z=1, z=2, x=1, x=2 and y=0 and the parabaloid y=x^2, I would say the region is given by

$$1 \leq x \leq 2$$
$$0 \leq y \leq x^2$$
$$1 \leq z \leq 2$$

It would make no sense to say

$$f(x,y,z)= \left\{\begin{array}{lr}1 \leq x \leq 2 \\ 0 \leq y \leq x^2 \\1 \leq z \leq 2 \end{array}\right.$$

You can't set a function equal to an inequality or set of inequalities, and you can't describe a 3D region by a function.

Im calling $$\phi,\theta,\rho$$ this way:

[PLAIN]http://www.math.montana.edu/frankw/ccp/multiworld/multipleIVP/spherical/convert3d.gif

And $$\rho\geq{0}$$

Okay, then you have:

$$\rho = \sqrt{x^2+y^2+z^2}$$
$$\phi = \cos^{-1}\left(\frac{z}{\sqrt{x^2+y^2+z^2}}\right)$$
$$\theta = \tan^{-1}\left(\frac{y}{x}\right)$$

 

[Telemachus]

Here it is:

$$x>0$$
$$y>0$$
$$x^2+y^2\leq{\frac{z^2}{3}}\forall{}z\in{[\frac{\sqrt[ ]{3}}{2}},\sqrt[ ]{3}]}$$
$$x^2+y^2+z^2\leq{4}\forall{z\in{(\sqrt[ ]{3},2]}}$$
$$x^2+y^2+z^2\geq{1}$$

Sorry, it took some time to make the draw. Anyway, its limited by the planes zy and zx, and by the sphere x²+y²+z²=1.

Thanks, I'll follow your indications.