Explaining a signal converting circuit

[gony rosenman]

i have a drawing of a circuit that converts a signal in range [-5,5] V to a range [0,1.2]V .
i wish to understand how it works..
i have basic knowledge of electricity as an undergraduate in general physics but a bit rusty , thus i am here looking for answers...

 

[lewando]

It is a "resistive summer" or "passive averager" described in this https://www.allaboutcircuits.com/textbook/semiconductors/chpt-8/averager-summer-circuits/.

 

[analogdesign]

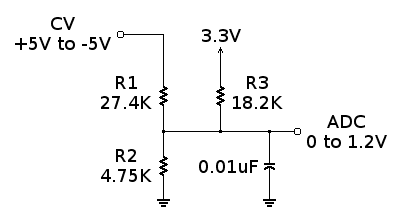
It is indeed a resistive summer. To see that it works (not HOW it works), you can write a nodal analysis equation (using Kirchhoff's current law) at node "ADC" and you will find it gives the function:

ADC = 0.12*CV + 0.6, as desired.

But you want to know HOW it works, here is a more intuitive explanation that is more in the spirit of how an analog engineer would approach the problem (rather than showing you a plug-and-chug simplification of a node equation).

First you need to appreciate that to do the level shifting you really want to do two different things. First, you want to set the "analog ground", or average value, to 0.6 (because that is midway between 0 and 1.2V). Second, you want to attenuate the magnitude of the CV range from 10 V (that is, 5V - (-5V) )to 1.2V. In other words, you want to multiply CV by a gain of 1.2 / 10 = 0.12 and shift its DC level from 0 to 0.6.

OK. Now, to see how the circuit works to do these things we invoke the principle of superposition. This principle states that if we have a linear system then we can calculate the response to each source independently, setting the other sources to zero (in this case CV and the 3.3 V supply) and then add them to get the composite response.

So, we get the baseline by looking at the 3.3 V supply. From the point of view of the 3.3 V supply, we see the 27.4 k and 4.75 k resistors are in parallel (remember we set CV = 0 here). Then, we have a voltage divider and ADC = ((4.75 || 27.4) / ( (4.75 || 27.4) + 18.2)) * 3.3. Now, 4.75 || 27.4 = 4.05 so we have ADC = (4.05 / ( 4.05 + 18.2))* 3.3 = 0.18 *3.3 = 0.6, as desired.

We get the attenuation by looking at what CV "sees". In this case, the 4.75k resistor is in parallel with the 18.2k resistor (remember we set the 3.3 volt source to 0 here). Then we proceed as above, ADC =((4.75 || 18.2) / ( (4.75 || 1.8) + 27.4)) * CV. Or, calculating it out, ADC = 0.12 * CV.

Adding the two responses together (invoking the principle of superposition) we have:

ADC = 0.12*CV + 0.6, which is exactly what we wanted in the first place.

Make sense?

 

[gony rosenman]

you , my dear sir , are an angel !
thank you for the clear and thorough explanation .
much appreciated