- #1
Shirish
- 244
- 32
I'm reading 'Core Principles of Special and General Relativity' by Luscombe - the part on parallel transport.
Initially we consider a vector field ##A## with components ##A^{\mu}## and we start at some point ##p\in U## with coordinates ##x^{\nu}##. The change in ##A^{\mu}##, according to the text, is ##-\Gamma^{\mu}_{\ \ \beta\nu}A^{\beta}(p)\text{d}x^{\nu}##.
But from parallel transport condition, we have ##\partial_{\nu}A^{\mu}(p)=-\Gamma^{\mu}_{\ \ \beta\nu}A^{\beta}(p)## and so, from what the book says, $$\begin{align}
\delta A^{\mu}\equiv\partial_{\nu}A^{\mu}(p)\ \text{d}x^{\nu}&=\text{d}A^{\mu}(p)
\end{align}$$
It seems like I can interpret the differential of ##A^{\mu}## at ##p##, i.e. ##\text{d}A^{\mu}(p)## as the change in value of ##A^{\mu}## as I incrementally move from ##p=x^{\nu}## to ##p'\equiv x^{\nu}+\text{d}x^{\nu}##.
But if you look at the figure, ##A^{\mu}+\text{d}A^{\mu}## and ##A^{\mu}+\delta A^{\mu}## are different, and so ##\text{d}A^{\mu}## and ##\delta A^{\mu}## are different, contradicting the equation I wrote above.
Where am I going wrong?
I guess ##U^{\beta}## and ##v## are vector fields instead of vectors as claimed in the quote. Till here I can understand, but then it's written:A vector ##v## given at every point of ##\gamma(\lambda)## with tangent vector ##U^{\beta}## is said to be parallel transported if the covariant derivative vanishes at all points of ##\gamma(\lambda)##: $$U^{\mu}\nabla_{\mu}v^{\alpha}=U^{\mu}(\partial_{\mu}v^{\alpha}+\Gamma^{\alpha}_{\ \ \rho\mu}v^{\rho})=0$$
I want to clarify my understanding of the part in bold. My current interpretation is: we can talk about the value of connection coefficients ##\Gamma^{\mu}_{\ \ \beta\nu}## _only in reference to some chart_, so let that chart be ##(U,x)##.Armed with the knowledge of parallel transport, we can complete the picture of the covariant derivative. Let ##\delta A^{\mu}\equiv -\Gamma^{\mu}_{\ \ \beta\nu}A^{\beta}\text{d}x^{\nu}## denote the change in ##A^{\mu}## that occurs in parallel transport through ##\text{d}x^{\nu}## (see fig below).
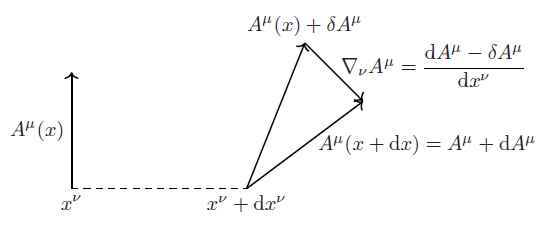
Initially we consider a vector field ##A## with components ##A^{\mu}## and we start at some point ##p\in U## with coordinates ##x^{\nu}##. The change in ##A^{\mu}##, according to the text, is ##-\Gamma^{\mu}_{\ \ \beta\nu}A^{\beta}(p)\text{d}x^{\nu}##.
But from parallel transport condition, we have ##\partial_{\nu}A^{\mu}(p)=-\Gamma^{\mu}_{\ \ \beta\nu}A^{\beta}(p)## and so, from what the book says, $$\begin{align}
\delta A^{\mu}\equiv\partial_{\nu}A^{\mu}(p)\ \text{d}x^{\nu}&=\text{d}A^{\mu}(p)
\end{align}$$
It seems like I can interpret the differential of ##A^{\mu}## at ##p##, i.e. ##\text{d}A^{\mu}(p)## as the change in value of ##A^{\mu}## as I incrementally move from ##p=x^{\nu}## to ##p'\equiv x^{\nu}+\text{d}x^{\nu}##.
But if you look at the figure, ##A^{\mu}+\text{d}A^{\mu}## and ##A^{\mu}+\delta A^{\mu}## are different, and so ##\text{d}A^{\mu}## and ##\delta A^{\mu}## are different, contradicting the equation I wrote above.
Where am I going wrong?

