- #1
adjacent
Gold Member
- 1,552
- 63
Homework Statement
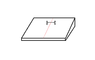
Let the angle of the block(slope) to be 30°.
height=0.6m, length=1m. Breadth=1m
Smallest height on diagram is 0m
Let the red line to divide the block by 2(when viewed from the top)
The two wheels are of equal diameter and is connected by a rod.
The total mass of two wheels + rod is 1kg.
Let the angle be measured from the red line.(At the image,the wheel system is 90° to the line)
1-Rotate the wheel to 0°.
It will not move.
2-Rotate to 90°
it will fall at maximum speed.
3- Rotate to 45°
will be slower than 90°.
So I am thinking of the relation between the angle and the speed of fall.
Homework Equations
##F=ma##
...
The Attempt at a Solution
Sorry I am at Gr.10. So I haven't studied vectors,forces or speeds at angles.
-Just curious-