Como Bluff
- 3
- 0
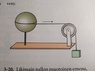
How do I calculate the acceleration of the falling weight? It is hanging from a string which goes through a wheel, and is attached to a sphere with thin walls. The string doesn't stretch and the wheel and the sphere spin without friction.
The fact that the weight is connected to multiple masses is the problem. How does one calculate the net moment of inertia that is affecting the acceleration of the falling weight?
For the sake of simplicity, I left out the values given in the original statement of the problem; these are of course available upon request.
The moments of inertia for the objects in the problem:
Jsphere = \frac{2}{3}mr2
Jwheel = \frac{1}{2}mr2
Thanks!
The fact that the weight is connected to multiple masses is the problem. How does one calculate the net moment of inertia that is affecting the acceleration of the falling weight?
For the sake of simplicity, I left out the values given in the original statement of the problem; these are of course available upon request.
The moments of inertia for the objects in the problem:
Jsphere = \frac{2}{3}mr2
Jwheel = \frac{1}{2}mr2
Thanks!