Field along vertical axis to hemispherical shell

[user240]

Homework Statement

A hemispherical shell has radius $R$ and uniform charge density $\sigma$. FInd the electric field at a point on the symmetry axis, at position $z$ relative to the center, for any $z$ value from $-\infty$ to $\infty$.

The Attempt at a Solution

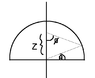
Let $\theta$ be the angle from the horizontal axis and $r$ be the distance from a point on the vertical axis to a point on the shell. By the cosine rule,

$$r^2=R^2+z^2-2zRcos(\frac{\pi}{2}-\theta) = R^2+z^2-2zRsin(\theta)$$.

The charge on a ring of the shell is $dQ=2\pi R^2cos(\theta)d\theta$. Because of the symmetry of the shell, the horizontal components of the field cancel along the center axis so to take only the vertical component, we'll put in a factor of $cos(\phi)$. From the sine rule,

$$\frac{R}{sin(\phi)} = \frac{r}{sin(\frac{\pi}{2} - \theta)} = \frac{r}{cos(\theta)}$$.

Therefore,

$$cos(\phi) = (1-\frac{R^2}{r^2}cos^2(\theta))^{1/2}$$

$$= \frac{(r^2-R^2cos^2(\theta))^{1/2}}{r}$$

Now putting back in the expression for $r$ in the numerator,

$$cos(\phi)=\frac{(R^2+z^2-2zRsin(\theta)-R^2cos^2(\theta))^{1/2}}{r}$$

Factoring out $R^2$ and replacing $1-cos^2(\theta)$ with $sin^2(\theta)$,

$$cos(\phi) = \frac{(R^2sin^2(\theta)-2zRsin(\theta)+z^2)^{1/2}}{r}$$

Now I can factor the numerator in two ways, so either I get

$$cos(\phi)= \frac{((z-Rsin(\theta))^2)^{1/2}}{r}=\frac{z-Rsin(\theta)}{r}$$

or

$$cos(\phi) = \frac{((Rsin(\theta)-z)^2)^{1/2}}{r}=\frac{Rsin(\theta)-z}{r}$$

(I guess this is the same as taking either positive or negative square root?)

If I go with the first option, the integral I get (omitting constants) is

$$\int_0^\frac{\pi}{2} \frac{cos(\theta)(z-Rsin(\theta))}{(z^2+R^2-2zRsin(\theta))^{3/2}}d\theta$$

whose solution is

$$\frac{z-R}{z^2\sqrt{z^2-2Rz+R^2}}+\frac{R}{z^2\sqrt{R^2+z^2}}$$

This seems to agree with the given solution - the second option would've given me a solution with second term being negative.

My first question is how do I know which to choose?

Second question is, the solution says that the first term is either positive or negative depending on whether $z$ is bigger or smaller than $R$. However, since you can factor the denominator to get $\sqrt{(z-R)^2}$, can you just argue that it's either positive or negative depending on whether you take the positive or negative root?

Finally, please point out any dodgy reasoning!

Thanks.

 

[kuruman]

However, since you can factor the denominator to get $\sqrt{(z-R)^2}$, can you just argue that it's either positive or negative depending on whether you take the positive or negative root?

You can argue that $\sqrt{(z-R)^2} = |z-R|.$ This is equal to $z - R$ when $z > R$ and $R-z$ when $z<R.$ There is no "plus or minus" here. The radical is a positive quantity since it does not a have a negative sign in front of it.