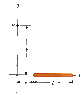Find an expression for the electric potential at P

[Keithkent09]

The thin, uniformly charged rod shown in the figure below has a linear charge density λ. Find an expression for the electric potential at P. (Use k_e for ke, lambda for λ, a, b, and L as necessary.)

Homework Equations

dV=k*dq/r
lambda*dx=dq

The Attempt at a Solution

I integrated using the above equations and went from 0 to L. I thought this was the right way to do it but I keep getting the wrong answer.

 

[Winzer]

Hello Keithkent09.

First: Show us your work and what you got for your integral.
When you integrate your potential equation you are integrating over the
location of charge correct? The integration does not happen from 0 to L. Your
charge location is not from 0 to L do you see? What should it be?

 

[Keithkent09]

the integral of (k*dq)/r=(k*lambda+dx)/r
r=sqrt(b^2+(a+x)^2) so...
k*lambda*dx/(sqrt(b^2+(a+x)^2))...and was not sure what to do after this

 

[Redbelly98]

The next step would be to do the integral. However ...

...here is a suggestion: let x=0 at the point directly below P. That will simplify the integral somewhat. Of course, this will change the limits on x: instead of 0 to L it will be ____ to ____ instead.

 

[Keithkent09]

Will the limits be from 0 to a+L?
Also if x=0 under point P how does that make the integral any easier, does that mean that x is thrown out in the integral and all that remains is the dx?

 

[Redbelly98]

Will the limits be from 0 to a+L?

If x=0 under point P, then the rod will lie between x=a and x=a+L, right?

Also if x=0 under point P how does that make the integral any easier, does that mean that x is thrown out in the integral and all that remains is the dx?

Well, set up the integral, using the approach you did before:

Homework Equations

dV=k*dq/r
lambda*dx=dq

What expression do you get for the integral in this case?

 

[Keithkent09]

is it just the integral of (k*lambda*dx)/(sqrt(a^2+b^2) from a to a+L?

 

[Redbelly98]

is it just the integral of (k*lambda*dx)/(sqrt(a^2+b^2) from a to a+L?

Not quite, the (sqrt(a^2+b^2) part is wrong. There should be an x in there somewhere.

Note, this term is equivalent to r, the distance from point P to some point along the wire. The point on the wire would be a distance x from the origin directly below P.

 

[Keithkent09]

Earlier I said that the denominator was sqrt(b^2+(a+x)^2) i do not understand why the placement of x=0 changes that up.

 

[Redbelly98]

Never mind, let's go back to your expression which was correct and not confusing you:

the integral of (k*dq)/r=(k*lambda+dx)/r
r=sqrt(b^2+(a+x)^2) so...
k*lambda*dx/(sqrt(b^2+(a+x)^2))...and was not sure what to do after this

This needs to be integrated from x=0 to x=L.
Try looking it up in a table of integrals.
The following might be useful for doing this integral: try a change of variable, u=a+x.