Find frequency of oscillating electron in electric field

[gacky27]

Homework Statement

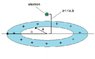
An electron is released from rest in an electric field (see picture attachment, it should explain everything). Upon release, it will oscillate due to the positive electric field. Find the frequency with which it oscillates.

Homework Equations

Coulomb's Law
Equation of an electrostatic field

The Attempt at a Solution

First, I found the electric field. I then used Coulomb's Law to find the force exerted by the field on the electron. I'm a little stuck from this point on.

 

[Redbelly98]

Welcome to Physics Forums.

Please show your results so far! What is the force on the electron that you derived?

Once you have the force, use the assumption z«a,b to get an approximate, simpler expression.

 

[gacky27]

I've actually tried that. It turns out to be zero when I do that, which can't be right. My result for E was:

-(σ/2εo)[(z/b)-(z/a)]

If I plug in z<<a,b I just get zero

My initial train of thought was to find E, use F=qE, then go from there.

Perhaps the value for E i found is wrong? I'll have to go back and redo it I guess.

 

[Redbelly98]

I've actually tried that. It turns out to be zero when I do that, which can't be right. My result for E was:

-(σ/2εo)[(z/b)-(z/a)]

If I plug in z<<a,b I just get zero

My initial train of thought was to find E, use F=qE, then go from there.

Perhaps the value for E i found is wrong? I'll have to go back and redo it I guess.

That looks good so far.

Can you rewrite your expression for E, so that it is

E = something × z​

Eventually, you want to come up with a force for the electron in the form:

F = - k z​

where k is a constant expression involving σ, ε_o, etc.