Find Hinge Force of Rod Undergoing Circular Motion

[utkarshakash]

Homework Statement

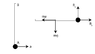
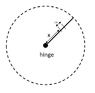
A rod of mass m and length l is hinged about its end A and is vertical initially. Now the end A is accelerated horizontally with acceleration a=g m/s^2. The hinge reaction when the rod becomes horizontal is ?

Homework Equations

See the attached picture for relevant diagrams.

The Attempt at a Solution

When viewed from the frame of the hinge, the rod experiences a pseudo force = ma. Since the rod undergoes circular motion about the hinge A,

R_x - ma = m \omega ^2 l

where omega is the angular velocity of the rod when it becomes horizontal. Now I don't know what to write regarding the vertical forces. I'm sure they do not balance each other. Also how do I find omega at the instant?

 

[paisiello2]

Shouldn't l be l/2 in your equation?

I think the vertical forces do balance out so that should be easy.

My suggestion would be to use conservation of energy to get ω.

 

[utkarshakash]

Shouldn't l be l/2 in your equation?

I think the vertical forces do balance out so that should be easy.

My suggestion would be to use conservation of energy to get ω.

Why should it be l/2? If I balance the vertical forces I get R(y) = mg which is wrong according to the answer key.

 

[paisiello2]

The center of mass is located at l/2.

You forgot to include the ma_y of the rod. If you take moments about the hinge then this will cancel with mg leaving R_y = 0.

 

[utkarshakash]

The center of mass is located at l/2.

You forgot to include the ma_y of the rod. If you take moments about the hinge then this will cancel with mg leaving R_y = 0.

But the rod undergoes circular motion about the hinge and not about its COM. R_y is not equal to zero, though.

 

[hav0c]

Can you please clarify whether the rod is in equilibrium in its horizontal position or is it undergoing a circular motion.

 

[utkarshakash]

Can you please clarify whether the rod is in equilibrium in its horizontal position or is it undergoing a circular motion.

The question says that the hinge is being moved. So, I think the rod should undergo circular motion about the hinge. The motion of the rod is a combination of rotational and translational motion when seen from ground. Am I wrong?

 

[Chestermiller]

The question says that the hinge is being moved. So, I think the rod should undergo circular motion about the hinge. The motion of the rod is a combination of rotational and translational motion when seen from ground. Am I wrong?

No. You're correct.

This is not a simple problem, but I can help you work your way through it.

The first thing I always do on a problem like this is to focus on the kinematics of the motion. Let x(t) be the horizontal displacement of the hinge at time t, and let θ(t) be the counterclockwise angle that the rod makes with the vertical y direction. (At time zero, x(0) = 0 and θ(0) = 0.) In terms of x and θ, what are the coordinates x_c and y_c of the center of mass of the rod at time t? What are the x and y components of the velocity of the center of mass of the rod at time t? What are the x and y components of the acceleration of the center of mass of the rod at time t? In terms of θ, what is the angular velocity ω and the angular acceleration α of the rod?

Now you are ready to do force and moment balances on the rod. For an arbitrary value of θ, what are the force balances in the x and y directions? What is the moment balance around the center of mass of the rod?

Incidentally, happy π day everyone.

Chet

 

[paisiello2]

But the rod undergoes circular motion about the hinge and not about its COM. R_y is not equal to zero, though.

Yes, you are right, I'm sorry about that. What I should have said was:

ma_y = mlα/2

where α is the angular acceleration

Take moments about the hinge to solve for α and substitute into the equation for summing forces in the Y direction.

 

[Chestermiller]

Yes, you are right, I'm sorry about that. What I should have said was:

ma_y = mlα/2

where α is the angular acceleration

Take moments about the hinge to solve for α and substitute into the equation for summing forces in the Y direction.

The angular velocity around the center of mass is the same as the angular velocity around the hinge. Just consider the angle that the rod makes with the vertical direction at any point along the rod. It's the same at all locations along the rod.

Chet

 

[paisiello2]

Yes, but taking moments about the hinge eliminates the reaction forces and makes the math simpler I think.

 

[Chestermiller]

Yes, but taking moments about the hinge eliminates the reaction forces and makes the math simpler I think.

OK. Let's see how it plays out. But, don't forget that, for a rigid body, the F = ma equation only applies to the acceleration of the center of mass.

Chet

 

[utkarshakash]

Yes, you are right, I'm sorry about that. What I should have said was:

ma_y = mlα/2

where α is the angular acceleration

Take moments about the hinge to solve for α and substitute into the equation for summing forces in the Y direction.

I could easily get R_y by your method but I'm still having trouble figuring out R_x. Here's what I did:

Initial Potential Energy of the rod = mgl/2 (assuming hinge to be at zero potential)
Let's say the rod acquires a linear velocity v when it becomes horizontal and angular velocity ω.

Final Energy = \dfrac{ml^2 \omega ^2}{6} + \dfrac{mv^2}{2}

But the problem is that there is no simple relation between v and ω and thus, I'm left with two variables.

 

[paisiello2]

I think we can set v_y = 0 considering pure rotation.

 

[Chestermiller]

The moment balance on the rod gives:
mg\frac{l}{2}sinθ=Iα=\left(\frac{ml^3}{3}\right)\frac{d^2θ}{dt^2}
where θ is the angle of the rod measured clockwise from the vertical. Rearranging this gives:
\frac{d^2θ}{dt^2}=\frac{3g}{2l}\sinθ
If we multiply both sides of this equation by dθ/dt, and integrate with respect to t, we obtain:
\left(\frac{dθ}{dt}\right)^2=\frac{3g}{l}(1-\cosθ)
When θ=π/2, these equations reduce to:

α=\frac{3g}{2l}
ω^2=\frac{3g}{l}

I think these results might help.

Chet

 

[paisiello2]

Not necessary to do all the integration and stuff. Just take moments directly when θ=90° and you get the same answer.

 

[Chestermiller]

Not necessary to do all the integration and stuff. Just take moments directly when θ=90° and you get the same answer.

Really. That's interesting. How did you get the equation for ω² without integrating?

Chet

 

[paisiello2]

I see what you mean. I guess you are solving a differential equation then.

 

[Chestermiller]

I see what you mean. I guess you are solving a differential equation then.

Yes, exactly.

This could also be viewed as a balance between rotational kinetic energy of the rod and gravitational potential energy of the rod, although, to be perfectly frank, it isn't obvious to me how this can be separated in some rational way from the overall mechanical energy balance on the rod. That's an issue that you and the OP were grappling with.

Chet

 

[utkarshakash]

The moment balance on the rod gives:
mg\frac{l}{2}sinθ=Iα=\left(\frac{ml^3}{3}\right)\frac{d^2θ}{dt^2}
where θ is the angle of the rod measured clockwise from the vertical. Rearranging this gives:
\frac{d^2θ}{dt^2}=\frac{3g}{2l}\sinθ
If we multiply both sides of this equation by dθ/dt, and integrate with respect to t, we obtain:
\left(\frac{dθ}{dt}\right)^2=\frac{3g}{l}(1-\cosθ)
When θ=π/2, these equations reduce to:

α=\frac{3g}{2l}
ω^2=\frac{3g}{l}

I think these results might help.

Chet

Shouldn't the torque due to pseudo force = ma be included as well?

 

[Chestermiller]

Shouldn't the torque due to pseudo force = ma be included as well?

A pseudo force is not a force. The moment balance is only supposed to include real forces.

Chet

 

[Saitama]

Hi Chestermiller!

I tried the problem following way.

The x-coordinate of CM of rod at any time is:
$$x(t)=\frac{1}{2}gt^2-\frac{l}{2}\sin\theta$$
From Newton's second law:
$$R_x=m\frac{d^2x}{dt^2}$$
Similarly I can write y(t) for CM of rod and then write:
$$mg-R_y=m\frac{d^2y}{dt^2}$$
But I feel what I have done is wrong, how do I introduce the acceleration in my equation given in the problem?

 

[Chestermiller]

Hi Chestermiller!

I tried the problem following way.

The x-coordinate of CM of rod at any time is:
$$x(t)=\frac{1}{2}gt^2-\frac{l}{2}\sin\theta$$
From Newton's second law:
$$R_x=m\frac{d^2x}{dt^2}$$
Similarly I can write y(t) for CM of rod and then write:
$$mg-R_y=m\frac{d^2y}{dt^2}$$
But I feel what I have done is wrong, how do I introduce the acceleration in my equation given in the problem?

The x and y coordinates of the center of mass is given by:
x_c(t)=x(t)-\frac{l}{2}\sinθ
y_c(t)=\frac{l}{2}\cosθ
where x(t) is the x coordinate of the hinge at time t.
From this, the velocity components of the center of mass are given by:
v_{cx}(t)=v(t)-\frac{l}{2}\cosθ\frac{dθ}{dt}
v_{cy}(t)=-\frac{l}{2}\sinθ\frac{dθ}{dt}
From this, the acceleration components of the center of mass are given by:
a_{cx}(t)=a-\frac{l}{2}\cosθ\frac{d^2θ}{dt^2}+<br /> \frac{l}{2}\sinθ\left(\frac{dθ}{dt}\right)^2
a_{cy}(t)=-\frac{l}{2}\sinθ\frac{d^2θ}{dt^2}-\frac{l}{2}\cosθ\left(\frac{dθ}{dt}\right)^2
where a is the acceleration of the hinge.
So, the force balances in the x and y directions can be written:
ma_{cx}=R_x
ma_{cy}=R_y-mg
Chet

 

[Saitama]

The x and y coordinates of the center of mass is given by:
x_c(t)=x(t)-\frac{l}{2}\sinθ
y_c(t)=\frac{l}{2}\cosθ
where x(t) is the x coordinate of the hinge at time t.

I am sorry if I am missing something but isn't that what I have written?

A few posts ago, you found $\omega^2$ as a function of $\theta$, I am wondering if it was necessary, can't we directly use energy conservation to find $\omega^2$ at $\theta=\pi/2$?

 

[Chestermiller]

I am sorry if I am missing something but isn't that what I have written?

A few posts ago, you found $\omega^2$ as a function of $\theta$, I am wondering if it was necessary, can't we directly use energy conservation to find $\omega^2$ at $\theta=\pi/2$?

I guess, yes, except for the g in the equation for x, rather than an a.

If you can find $\omega^2$ at $\theta=\pi/2$ with overall energy conservation, that would be great. Please show how? The only way I was able to do it was with the moment balance. Probably, I'm missing something.

Chet

 

[Saitama]

I guess, yes, except for the g in the equation for x, rather than an a.

The problem statement mentions that $a=g$. :)

If you can find $\omega^2$ at $\theta=\pi/2$ with overall energy conservation, that would be great. Please show how? The only way I was able to do it was with the moment balance. Probably, I'm missing something.

Chet

I did say "I am wondering". :P

I think you are right but please look at the following, something doesn't look right. :(

From energy conservation,
$$mg\frac{l}{2}=\frac{1}{2}\frac{ml^2}{3}\omega^2+\frac{1}{2}mv^2$$
$$\Rightarrow gl=\frac{l^2\omega^2}{3}+v^2$$
From the equations you wrote:
$$v^2=v^2_{cx}(t)+v^2_{cy}(t)=g^2t^2+\frac{l^2}{4}\omega^2-gtl\cos\theta \omega$$
At $\theta=\pi/2$, the above becomes:
$$v^2=g^2t^2+\frac{l^2}{4}\frac{3g}{l}=g^2t^2+\frac{3gl}{4}$$
Substituting in the energy equation and solving for $t^2$ gives a negative answer. :(

 

[Tanya Sharma]

Energy conservation can not be applied in this problem.

 

[Saitama]

Energy is definitely not conserved .

Erm...why not?

 

[Tanya Sharma]

Are you completely sure there is no work done by any force on the rod ?

 

[Saitama]

Are you completely sure there is no work done being done by any force on the rod ?

The external force which is accelerating the rod also does work on the rod, right?

 

[Tanya Sharma]

Correct...So forget energy conservation :)

 

[Saitama]

Correct...So forget energy conservation :)

Thanks! :)

 

[Tanya Sharma]

We need another equation apart from the last four equations by Chet in post#23

 

[Saitama]

We need another equation apart from the last four equations by Chet in post#23

Are you talking about this?

https://www.physicsforums.com/showpost.php?p=4689443&postcount=15

I think we don't need the equations from #23, page 1 of this thread has it all. Chestermiller derived $\omega^2$ and $\alpha$ as a function of $\theta$ in post #15 and I suppose that is sufficient. Next step is to apply Newton's second law.

 

[Tanya Sharma]

Are you talking about this?

https://www.physicsforums.com/showpost.php?p=4689443&postcount=15

I think we don't need the equations from #23, page 1 of this thread has it all. Chestermiller derived $\omega^2$ and $\alpha$ as a function of $\theta$ in post #15 and I suppose that is sufficient. Next step is to apply Newton's second law.

I may be wrong but I think the equation in post#15 is incorrect .You cannot write torque equation about the hinge .

In this problem it has to be written about the COM.

 

[utkarshakash]

I may be wrong but I think the equation in post#15 is incorrect .You cannot write torque equation about the hinge .

In this problem it has to be written about the COM.

You can write torque equation about either of them. Chestermiller took it about the hinge to make the reaction forces disappear in the torque equation and thus save a lot of work which was not possible otherwise. I don't find anything incorrect in his solution as it gives me the correct answer.

 

[paisiello2]

Correct...So forget energy conservation :)

Except we know what that work is as it is explicitly given in the problem. In this case the work done is only in one direction and if we are only interested in the rotational energy then we can solve directly for ω without doing any integration.

In addition, gravity also does work on the system. Therefore by your logic we could never do a conservation of energy which is not correct.

 

[utkarshakash]

Congrats for getting the correct answer .Quite a difficult problem .

Could you share exactly what equations you used and what is the correct answer ?

OK here's what I did:

Since Chet already figured out ω I used that to put it in this equation

R_x - mg = m \omega ^2 l

which gives R_x = 4mg

Since the rod rotates about the hinge,
a_y = \dfrac{\alpha l}{2}

Using the equation \tau = I \alpha
I get

\dfrac{mgl}{2} = \dfrac{ml^2}{3} \alpha

Now using Newton's second law

mg - R_y = ma_y

Solve the above equations and you'll get the answer.

 

[Saitama]

OK here's what I did:

Since Chet already figured out ω I used that to put it in this equation

R_x - mg = m \omega ^2 l

Why do you use $l$ instead of $l/2$?

 

[Saitama]

Okay, I have tried something which gives the correct answer of $\sqrt{257}mg/4$.

Move to the frame accelerating with an acceleration a=g. This results in a pseudo force of mg acting on the rod towards left.

Doing moment balance when the rod is at an angle $\theta$, gives:
$$ mg\frac{l}{2}\sin\theta+mg\frac{l}{2}\cos\theta=\frac{ml^2}{3}\alpha $$
Rewriting alpha as $\dfrac{1}{2}\dfrac{d\omega^2}{d\theta}$ and simplifying gives:
$$\frac{d\omega^2}{d\theta}=\frac{3g}{l}(\sin\theta+\cos\theta)$$
Solving the D.E gives:
$$\omega^2=\frac{3g}{l}(1-\cos\theta+\sin\theta)$$
At $\theta=\pi/2$, $\omega^2=6g/l$. From Newton's second law:
$$R_x-mg=m\omega^2\frac{l}{2} \Rightarrow R_x=4mg$$
This is the same value which utkarshakash posted and I am inclined to think that what I have done above makes more sense because I wrote $R_x-mg=m\omega^2\frac{l}{2}$ instead of $R_x-mg=m\omega^2l$. But then Chet said that we don't take into account the pseudo forces when taking moments.

EDIT: If I work in this accelerating frame, I can get the value of $\omega^2$ directly from energy conservation.

$$\frac{mgl}{2}+\frac{mal}{2}=mgl=\frac{1}{2}\frac{ml^2}{3}\omega^2$$
$$\Rightarrow \omega^2=\frac{6g}{l}$$

 

[paisiello2]

I may be wrong but I think the equation in post#15 is incorrect .You cannot write torque equation about the hinge .

In this problem it has to be written about the COM.

Not true. You can take any frame of reference you want. Taking moments about the hinge simplifies the problem.

 

[Chestermiller]

OK. I'm going to do this a another way, by taking moments about the center of mass. This should focus on Tanya's concern about taking moments about the hinge, and should also address utkarshakash and Pranav-Arora's contention that the pseudo force needs to be included if we take moments about the hinge. Taking moments about the center of mass gives:

R_x\frac{l}{2}\cosθ+R_y\frac{l}{2}\sinθ=\left(m\frac{l^2}{12}\right)<br /> \frac{d^2θ}{dt^2}

Note that, on the right hand side of this equation, I've used the moment of inertia about the center of mass. Now, from the force balance and the kinematics,
R_x=m\left(g-\frac{l}{2}\cosθ\frac{d^2θ}{dt^2}+<br /> \frac{l}{2}\sinθ\left(\frac{dθ}{dt}\right)^2\right)

R_y=mg-m\left(\frac{l}{2}\sinθ\frac{d^2θ}{dt^2}+\frac{l}{2}\cosθ\left(\frac{dθ}{dt}\right)^2\right)
Now if we substitute these equations for the reaction forces into the moment balance equation and combine terms, we obtain:
mg\frac{l}{2}\cosθ+mg\frac{l}{2}\sinθ=m\left(\frac{l^2}{3}\right)\frac{d^2θ}{dt^2}
This is identical to Pranav-Arora's equation in the previous post. So it looks like Tanya was right about the need to take moments about the center of mass, and utkarshakash and Pranav-Arora were right about the need to include the pseudo reaction force if you take moments about the hinge.

Chet

 

[Saitama]

Very nicely done, thanks a lot Chestermiller. Its always great to know about different ways to solve a problem.

I got to learn a lot from this thread, thanks to utkarshakash for putting up such an excellent problem. :)

 

[paisiello2]

So it looks like Tanya was right about the need to take moments about the center of mass, and utkarshakash and Pranav-Arora were right about the need to include the pseudo reaction force if you take moments about the hinge.

The pseudo forces or inertial forces are there regardless of what reference frame you pick. So it's wrong to say you have to take it only at the center of mass. I think using conservation of energy is another way to do it but doesn't involve solving a differential equation.

 

[utkarshakash]

Okay, I have tried something which gives the correct answer of $\sqrt{257}mg/4$.

Move to the frame accelerating with an acceleration a=g. This results in a pseudo force of mg acting on the rod towards left.

Doing moment balance when the rod is at an angle $\theta$, gives:
$$ mg\frac{l}{2}\sin\theta+mg\frac{l}{2}\cos\theta=\frac{ml^2}{3}\alpha $$
Rewriting alpha as $\dfrac{1}{2}\dfrac{d\omega^2}{d\theta}$ and simplifying gives:
$$\frac{d\omega^2}{d\theta}=\frac{3g}{l}(\sin\theta+\cos\theta)$$
Solving the D.E gives:
$$\omega^2=\frac{3g}{l}(1-\cos\theta+\sin\theta)$$
At $\theta=\pi/2$, $\omega^2=6g/l$. From Newton's second law:
$$R_x-mg=m\omega^2\frac{l}{2} \Rightarrow R_x=4mg$$
This is the same value which utkarshakash posted and I am inclined to think that what I have done above makes more sense because I wrote $R_x-mg=m\omega^2\frac{l}{2}$ instead of $R_x-mg=m\omega^2l$. But then Chet said that we don't take into account the pseudo forces when taking moments.

EDIT: If I work in this accelerating frame, I can get the value of $\omega^2$ directly from energy conservation.

$$\frac{mgl}{2}+\frac{mal}{2}=mgl=\frac{1}{2}\frac{ml^2}{3}\omega^2$$
$$\Rightarrow \omega^2=\frac{6g}{l}$$

But why should we use l/2 here? Since the rod rotates about the hinge, shouldn't it be l? It'd be nice if you could explain me.

 

[Chestermiller]

The pseudo forces or inertial forces are there regardless of what reference frame you pick. So it's wrong to say you have to take it only at the center of mass.

If you don't want to have to include a pseudo force, (and you are using an inertial frame of reference) then you have to take moments about the center of mass. Tanya already pointed out the error of not taking moments around the center of mass, and I confirmed Tanya's assertion in my most recent post.

I think using conservation of energy is another way to do it but doesn't involve solving a differential equation.

So far you've said that several times, but we still haven't seen your demonstration of how it can be done.

Of course, in the accelerated frame, doing it using energy conservation is no problem because there the pseudo force becomes an actual body force with a horizontal "graviational" potential (as reckoned by observers in the accelerated frame.)

Chet

 

[paisiello2]

If you don't want to have to include a pseudo force, (and you are using an inertial frame of reference) then you have to take moments about the center of mass. Tanya already pointed out the error of not taking moments around the center of mass, and I confirmed Tanya's assertion in my most recent post.

That's not what I said. What I said was the inertia forces are there regardless of what reference frame you choose. So Tanya made an erroneous statement.

 

[Saitama]

But why should we use l/2 here? Since the rod rotates about the hinge, shouldn't it be l? It'd be nice if you could explain me.

Lets consider a rod of mass m rotating with a constant angular velocity $\omega$. In the rotating frame, a centrifugal force acts on it. Consider a small length ($dx$) of rod at a distance x from the hinge. The centrifugal force on it is given by $(m/l)\omega^2x\,dx$. Integrating to calculate the net centrifugal force gives $m\omega^2l/2$ which is the result I used in the problem.

I hope that helps.

 

[Saitama]

That's not what I said. What I said was the inertia forces are there regardless of what reference frame you choose. So Tanya made an erroneius statement.

Hi paisiello2!

How about writing down a few equations and see for yourself? ;)

 

[Tanya Sharma]

OK. I'm going to do this a another way, by taking moments about the center of mass. This should focus on Tanya's concern about taking moments about the hinge, and should also address utkarshakash and Pranav-Arora's contention that the pseudo force needs to be included if we take moments about the hinge. Taking moments about the center of mass gives:

R_x\frac{l}{2}\cosθ+R_y\frac{l}{2}\sinθ=\left(m\frac{l^2}{12}\right)<br /> \frac{d^2θ}{dt^2}

Note that, on the right hand side of this equation, I've used the moment of inertia about the center of mass. Now, from the force balance and the kinematics,
R_x=m\left(g-\frac{l}{2}\cosθ\frac{d^2θ}{dt^2}+<br /> \frac{l}{2}\sinθ\left(\frac{dθ}{dt}\right)^2\right)

R_y=mg-m\left(\frac{l}{2}\sinθ\frac{d^2θ}{dt^2}+\frac{l}{2}\cosθ\left(\frac{dθ}{dt}\right)^2\right)
Now if we substitute these equations for the reaction forces into the moment balance equation and combine terms, we obtain:
mg\frac{l}{2}\cosθ+mg\frac{l}{2}\sinθ=m\left(\frac{l^2}{3}\right)\frac{d^2θ}{dt^2}
This is identical to Pranav-Arora's equation in the previous post. So it looks like Tanya was right about the need to take moments about the center of mass, and utkarshakash and Pranav-Arora were right about the need to include the pseudo reaction force if you take moments about the hinge.

Chet

Brilliant...Simply brilliant !

Thank you so much Chet