LCSphysicist
- 644
- 162
- Homework Statement
- Pendulum plane, which suspension executes a harmonic motion.
- Relevant Equations
- \n
Pendulum plane, which suspension executes a horizontal harmonic motion $$x = acos(\gamma t)$$
Position P, orientation x to right and y points below, phi is the pendulum's angle wrt y.
$$P = (acos(\gamma t) + lsin(\phi(t)), lcos(\phi(t)) )$$
So executing all that is necessary, i found it, after eliminates explicit dependence (and only dependence) of time
$$\frac{m(l^2\dot{\phi }^{2} -2la\gamma \dot{\phi }cos(\phi )sin(\gamma t)) }{2} + mglcos(\phi )$$
BUt the answer is:
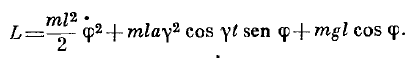
Not sure about this middle term, is it right?
Position P, orientation x to right and y points below, phi is the pendulum's angle wrt y.
$$P = (acos(\gamma t) + lsin(\phi(t)), lcos(\phi(t)) )$$
So executing all that is necessary, i found it, after eliminates explicit dependence (and only dependence) of time
$$\frac{m(l^2\dot{\phi }^{2} -2la\gamma \dot{\phi }cos(\phi )sin(\gamma t)) }{2} + mglcos(\phi )$$
BUt the answer is:
Not sure about this middle term, is it right?