You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Find the pressure p_1 due to a single particle
- Thread starter ~angel~
- Start date
AI Thread Summary
The discussion focuses on calculating the pressure p_1 due to a single particle, emphasizing the need to express it in terms of Boltzmann's constant (k_B), temperature (T), and the dimensions of a rectangular prism (L_x, L_y, L_z). Initial attempts using the ideal gas law were deemed incorrect due to the context of a single particle rather than moles. Participants clarify the definitions of the variables involved and confirm that the pressure can be derived from the relationship p = F/A, where force is related to momentum change. The final expressions for pressure are discussed, including p = (m*v_x)/V, highlighting the importance of understanding the dynamics of a single particle in a confined space. The conversation illustrates the complexities of applying thermodynamic principles to individual particles.
Physics news on Phys.org
whozum
- 2,219
- 1
Care to define those variables?
~angel~
- 150
- 0
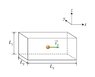
k_B is boltzmanns constant. If you look at the picture, you can see that L_x, L_y, and L_z are the length, width and height of the rectangular prism. T is the absolute temperature.
whozum
- 2,219
- 1
You can express V in terms of L_x, L_y, L_z
Is this mastering physics?
p = kT/V
No moles here, single particle.
Is this mastering physics?
p = kT/V
No moles here, single particle.
~angel~
- 150
- 0
Yeah, mastering physics. That's what stuffed me up- the moles. Thanks.
~angel~
- 150
- 0
Ok...I've now found the pressure for that, and I also found the pressure fon the wall due to a single particle whose squared speed in the x direction is v_x^2 [the answer to the later is (m*v_x)/V]. Now I need to find the pressure in terms of T, k and V, and any other given quantities, but I can't seem to get it.
whozum
- 2,219
- 1
Show me your work for finding the pressure for v_x, and v_x^2.
~angel~
- 150
- 0
p = F/A
The force is equal to dp(momentum)/dt = (2mv_x)/((2*L_x)/(v_x))
Area = Ly*Lz
Therefore, p = (m*v_x)/V
The force is equal to dp(momentum)/dt = (2mv_x)/((2*L_x)/(v_x))
Area = Ly*Lz
Therefore, p = (m*v_x)/V
Similar threads
- Replies
- 10
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 9
- Views
- 728
- Replies
- 5
- Views
- 1K
- Replies
- 10
- Views
- 2K
- Replies
- 116
- Views
- 6K
- Replies
- 5
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 2
- Views
- 2K
Hot Threads
-
The problem of one tube and two balls on a plane
- Started by crazy lee
- Replies: 60
- Introductory Physics Homework Help
-
Collision of a bullet on a rod-string system: query
- Started by palaphys
- Replies: 70
- Introductory Physics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math