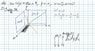s3a
- 814
- 8
Homework Statement
Find the volume of the region bounded by the planes 7x + 6y + 8z = 9, y = x, x = 0, z = 0.
Homework Equations
Multiple integration.
The Attempt at a Solution
My attempt at a solution is attached. To test, I computed the answer with Wolfram Alpha which yielded an incorrect answer of 243/5488.
Any help in solving this problem would be greatly appreciated!
Thanks in advance!