bayan
- 202
- 0
Hi,
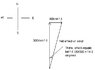
There is an aircraft moving at 300KM/h from its destination due north from an airport. It has to fly to the other airport(North) for 90KM.
The wind is blowing at 80KM/h from West to east.
At what angle must the aircraft fly to make its destination.
From my work out I found it to be N15.467W.
here is some work out.
let O=V wind
Let H=V aircraft
O/H=sin
Sin Thita=O/H
=80/300
Thita=Sin^1(80/300)
=Sin^-1(0.2667)
=15.467
Does this look right?
There is an aircraft moving at 300KM/h from its destination due north from an airport. It has to fly to the other airport(North) for 90KM.
The wind is blowing at 80KM/h from West to east.
At what angle must the aircraft fly to make its destination.
From my work out I found it to be N15.467W.
here is some work out.
let O=V wind
Let H=V aircraft
O/H=sin
Sin Thita=O/H
=80/300
Thita=Sin^1(80/300)
=Sin^-1(0.2667)
=15.467
Does this look right?