Heat
- 272
- 0
Homework Statement
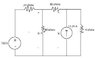
Hi I'm trying to solve the following using mesh current method, instead of node voltage.
For this I decided to use supermesh.
I made loop 1 the leftmost loop, and loop 2 combination of the center and right loop.
-150 + 20I1 + 80(I1-I2) = 0
40I2 = 4I2 = 80 (I2-I1) = 0
solving for this gives:
I1 = 3.10 A
I2 = 2 AI'm supposed to find v_1 and v_2. So since to find v_1, I do the following
3.10 - 2 = 1.1
V=IR = (1.1 A)(80 ohms) = 88 V <--------seems about right.
So now I'm trying to find v_2.
The only equations, I'm familiar is p = vi , p = i^2R v = ir. and since the current is given of 11.25 A for that portion.
V_2 = (11.25)(R)
I don't know how to proceed. I'm thinking about applying KVL, since voltage across a loop is 0.
which would be on second loop
-80(1.1 A)+40(2 A) + v_2 = 0
v_2 = 8 V <-----------I'm not sure if this is right, or if anything I did is right. :(
Circuit: http://imgur.com/LLno5.jpg
Attachments
Last edited: