ProBasket
- 140
- 0
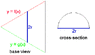
The base of a certain solid is an equilateral triangle with altitude 14. Cross-sections perpendicular to the altitude are semicircles. Find the volume of the solid, using the formula V= \int_a^{b} A(x)dx
applied to the picture shown attached to this post (click for a better view), with the left vertex of the triangle at the origin and the given altitude along the -axis.
i figure a= 0 and b = 14 and i will be plugging it into the formula pi*r^2 right?
the problem I'm having is finding the cross-section. can someone lend me a hand?
applied to the picture shown attached to this post (click for a better view), with the left vertex of the triangle at the origin and the given altitude along the -axis.
i figure a= 0 and b = 14 and i will be plugging it into the formula pi*r^2 right?
the problem I'm having is finding the cross-section. can someone lend me a hand?