jlmccart03
- 175
- 9
Homework Statement
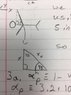
A skydiver is strapped to a rocket and shot into outer space. There is no air resistance so he is able to make his arms into a 45° angle with respect to his body and pretend they are "wings." To a stationary observer on the Moon (we will consider the Moon stationary for our purposes), at what angle will it appear that he is holding out his arms with respect to his body when he goes speeding by head-first in the -x direction at speed v = 0.6c?
Homework Equations
Length contraction or Lorentz transformation
The Attempt at a Solution
I think this is a Lorentz transformation, but I do not know how to get an angle theta. I only know of time dilation and length contraction niether have a theta in their equations so what am I missing?