Finding dipole moment / Electric Field Problem

In summary, the problem is that you don't seem to be capturing the charge, Q, correctly in your equation. You should try using a different variable of integration.
  • #1
puggleboy
1
0

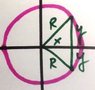
Homework Statement


Problem 3 from the attached photo

Homework Equations


p = qd

The Attempt at a Solution


I know the magnitude of the dipole moment is p = qd, where d is the distance between the 2 oppositely charged particles. I know the direction of the dipole moment vector is from - to +. My first thought is there's no charge separation, and hence a dipole moment equals zero. Something tells me this isn't the case.
 

Attachments

  • physics.png
    physics.png
    97 KB · Views: 417
Physics news on Phys.org
  • #2
I don't know why you think there is no charge separation. Some charges are R√2 from the nearest opposite charge. Only where the two semicircles meet is there no separation.
 
  • #3
Something like p = ∫dp = ∫∫dq⋅dr, where 0 ≤ r ≤ R ?
 
  • #4
Taulant Sholla said:
Something like p = ∫dp = ∫∫dq⋅dr, where 0 ≤ r ≤ R ?
The charges are along arcs, not distributed over semicircular areas, so I don't see how you get a double integral.
 
  • #5
What if I setup like this (attached), using:
p = ∫dp = q∫2y = 2q∫(R2-x2)0.5dx from R to -R? Don't I need to differentialize Q somehow?
 

Attachments

  • Picture1.jpg
    Picture1.jpg
    10.5 KB · Views: 335
  • #6
Taulant Sholla said:
What if I setup like this (attached), using:
p = ∫dp = q∫2y = 2q∫(R2-x2)0.5dx from R to -R? Don't I need to differentialize Q somehow?
That integral should work, but you will find it easier in polar coordinates. I don't know what you mean by "differentialize Q".
 
  • #7
So, using...
Picture2.jpg

...would we use d = charge separation = 2R, not d=R?

So, p = ∫dp = ∫d(dq) = ∫(2R)dq = ∫(2R)[λRdθ]

Where λ=Q/s, so Q = λs, or dq=λds=λRdθ, resulting in...

So, p = 2λR2∫dθ from pi to -pi?

This isn't feeling right since nothing is mentioned about charge density...??
 
  • #8
Taulant Sholla said:
So, using...
View attachment 95140
...would we use d = charge separation = 2R, not d=R?

So, p = ∫dp = ∫d(dq) = ∫(2R)dq = ∫(2R)[λRdθ]

Where λ=Q/s, so Q = λs, or dq=λds=λRdθ, resulting in...

So, p = 2λR2∫dθ from pi to -pi?

This isn't feeling right since nothing is mentioned about charge density...??
No, the integral you have now won't work. The dipole moment is a vector. Integration is a sum, so when you integrate vectors you need that sum to reflect vector addition. Your diagram above pairs charges in such a way that the dipoles willpoint in different directions.
Your previous way of pairing them was fine, and so was the integral you wrote down. You just need to rewrite that integral in polar form.
 
  • #9
That was my attempt at re-writing in polar form... which apparently is incorrect. I'm staring at...
Picture1.jpg

If I try x=Rcosθ, y=Rsinθ
  1. p = ∫dp
  2. = ∫(Q)(2y)
  3. = 2Q∫Rsinθdθ
  4. = -2QRcosθ
  5. eval'd from 0 to pi?
For #2, don't I need a variable of integration? If I use dy, rather than y, I'd get a sine term in #4, which would result in an answer of zero - which I'm pretty sure isn't correct?
Also, still doesn't seem like I'm capturing the charge, Q, correctly via this method?
 
  • #10
Unless I integrate from π/2 to -π/2... ?
 
  • #11
ρρ
Taulant Sholla said:
That was my attempt at re-writing in polar form... which apparently is incorrect. I'm staring at...
View attachment 95142
If I try x=Rcosθ, y=Rsinθ
  1. p = ∫dp
  2. = ∫(Q)(2y)
  3. = 2Q∫Rsinθdθ
  4. = -2QRcosθ
  5. eval'd from 0 to pi?
For #2, don't I need a variable of integration? If I use dy, rather than y, I'd get a sine term in #4, which would result in an answer of zero - which I'm pretty sure isn't correct?
Also, still doesn't seem like I'm capturing the charge, Q, correctly via this method?
In line 2, Q is the charge on a small element of arc, ρRdθ.
In line 3, you have correctly left the dθ inside the integral, so the Q outside is now ρR.
Other than that, your steps 1 to 5 are correct. It does not give zero.
 
  • #12
okay - thank you *very* much for all your help!
 
  • #13
Taulant Sholla said:
okay - thank you *very* much for all your help!
You are welcome. What was your final answer? Bear in mind that you were given the total charge on each arc, not the charge density.
 
  • #14
Right. I assume I'd use:
  1. ρ= Q/s
  2. = Q/(2πR)/2, or
  3. ρ = Q/(πR)?
 
  • #15
Taulant Sholla said:
Right. I assume I'd use:
  1. ρ= Q/s
  2. = Q/(2πR)/2, or
  3. ρ = Q/(πR)?
Good.
 

FAQ: Finding dipole moment / Electric Field Problem

1. What is a dipole moment?

A dipole moment is a measure of the separation of positive and negative charges in a molecule. It is a vector quantity that is calculated by multiplying the magnitude of the charge by the distance between the charges.

2. How is dipole moment calculated?

Dipole moment can be calculated by multiplying the magnitude of the charge by the distance between the charges. This distance is typically measured in angstroms (Å), and the charge is measured in coulombs (C).

3. What is the relationship between dipole moment and electric field?

The electric field is a measure of the force exerted on a charged particle. The direction of the electric field is in the direction of the force that would be exerted on a positive test charge. The dipole moment is related to the electric field by the equation p = qd, where p is the dipole moment, q is the magnitude of the charge, and d is the distance between the charges.

4. How can dipole moment be used to determine the polarity of a molecule?

The dipole moment of a molecule is a measure of the separation of positive and negative charges. If the dipole moment is non-zero, the molecule is polar, meaning it has a positive end and a negative end. If the dipole moment is zero, the molecule is nonpolar, meaning the charges are evenly distributed and there is no separation of charges.

5. What factors affect the dipole moment of a molecule?

The dipole moment of a molecule is affected by the magnitude of the charge, the distance between the charges, and the orientation of the charges. In general, a larger separation between charges and a larger magnitude of charge will result in a larger dipole moment. The orientation of the charges can also affect the dipole moment, as a molecule with a bent shape may have a larger dipole moment than a linear molecule with the same charges and separation.

Similar threads

Why is a current ring approx a magnetic dipole from very far off?
Replies
7
Views
729
Electric dipole moment vs electric current dipole moment
Replies
1
Views
1K
External forces required to move an electric dipole quasi-statically
Replies
14
Views
879
Dipole placed in a uniform electric field
Replies
11
Views
2K
Understanding the energy of a dipole in a uniform electric field
Replies
2
Views
2K
Dipole moment, electric potential
Replies
17
Views
2K
Calculation of magnetic dipole moment of the Earth
Replies
8
Views
397
Effect of different magnetic fields on a magnetic dipole
Replies
25
Views
731
What is the size of the magnetic dipole moment?
Replies
5
Views
1K
Finding the dipole moment of a molecule in an electric field
Replies
4
Views
6K

Hot Threads

Recent Insights

Back
Top