Finding Instantaneous UL and iL After Commutation for Transients (LC) Physics

[builder_user]

Homework Statement

Find instanteous UL, iL after commutation
Type of commutation - switch key

Homework Equations

The Attempt at a Solution

J=4*K1
L1=1mH*K2
C1=10mkF8*K2
R1=4*K3
R2=4*K3
R3=2*K3
K1=1.2
K2=0.7
K3=1

How to make it?

 

[builder_user]

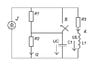
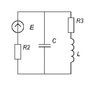
before commutation
Uc1(0_)=Uc1(0+)=0
UL1(0_UL1(0+)=0?

 

[builder_user]

I assume you should assume that the circuit is in steady state before the switch is closed.

If that is the case, no current will flow through the capacitor, and the inductor will be like a short circuit.

It means that all circuit will have only resistors?Ok.
After I'll find U on the capacitor and current through the inductor what to do next?

 

[MisterX]

I assume you should assume that the circuit is in steady state before the switch is closed.

If that is the case, no current will flow through the capacitor, and the inductor will be like a short circuit.

Solve that resistor network and get the voltage on the capacitor and the current through the inductor. Do these quantities change instantaneously? You should be able to get the instantaneous values at the moment of switch closure this way.

You could use the Laplace transform of the circuit after the switch is closed to get the transients.

 

[builder_user]

You could use the Laplace transform of the circuit after the switch is closed to get the transients.

How?

 

[MisterX]

Here's how:

Replace the circuit elements with their http://en.wikipedia.org/wiki/Laplace_transform#s-Domain_equivalent_circuits_and_impedances". Solve for the Laplace transform of the variables of interest. Then find the inverse Laplace transform of those variables. Alternatively, you could write out the differential equations.

 

[gneill]

The Attempt at a Solution

J=4*K1
L1=1mH*K2
C1=10mkF8*K2
:
:

Is that 8 a typo, or is it really 8*K2 ? These problems with the "K" constants seem a bit odd. Why not just specify the component values and be done with it? Also, are we to take the resistance values to have implied Ohms units? (the capacitors and inductors have specified millihenries and microfarads). The current, too, lacks explicit specification for units. Do we assume Amps and not milliamps?

 

[builder_user]

Here's how:

Replace the circuit elements with their http://en.wikipedia.org/wiki/Laplace_transform#s-Domain_equivalent_circuits_and_impedances". Solve for the Laplace transform of the variables of interest. Then find the inverse Laplace transform of those variables. Alternatively, you could write out the differential equations.

I need both methods.For Laplace I need to replace elems and for dif. I need not to replace sth?

 

[builder_user]

Is that 8 a typo, or is it really 8*K2 ? These problems with the "K" constants seem a bit odd. Why not just specify the component values and be done with it? Also, are we to take the resistance values to have implied Ohms units? (the capacitors and inductors have specified millihenries and microfarads). The current, too, lacks explicit specification for units. Do we assume Amps and not milliamps?

10mkF*K2

Before commutation and after inductor Ul(0).But what's happen with capacitor?After commutation it seems that there is no current in his circuit.

 

[builder_user]

It's the last task.
What's happen with capacitor?

I need to find Thevenin equivavalent before and after commutation right?

 

[gneill]

It's the last task.
What's happen with capacitor?

I need to find Thevenin equivavalent before and after commutation right?

The capacitor will have some initial voltage on it when the switch is closed. The inductor will be carrying some initial current.

Are you required to find U(t) and i(t) for the inductor in the problem, or just the initial values after the switch closes? Otherwise, since there's both L and C in the circuit there will probably be some oscillation after the switch closes; you might have to deal with damped oscillation (second order differential equation rather than first order).

You can probably skip finding the Thevenin equivalent for the 'before' circuit if you can determine the voltage on the capacitor and current through the inductor before the switch is closed.

 

[builder_user]

The capacitor will have some initial voltage on it when the switch is closed. The inductor will be carrying some initial current.

Are you required to find U(t) and i(t) for the inductor in the problem, or just the initial values after the switch closes? Otherwise, since there's both L and C in the circuit there will probably be some oscillation after the switch closes; you might have to deal with damped oscillation (second order differential equation rather than first order).

You can probably skip finding the Thevenin equivalent for the 'before' circuit if you can determine the voltage on the capacitor and current through the inductor before the switch is closed.

The same task as in previous topic.But for circuits with capacitor and inductor.Before "switch is closed" in the circuit will be capacitor and inductor?Or only capacitor?

 

[gneill]

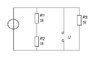
Before the switch is closed:

The capacitor will be charged to some constant value, it will be passing no current.
The inductor will be passing some constant current, it will have no voltage drop.

After the switch is closed:

The switch will short circuit R1, so R1 "disappears". This leaves R2, C1 and R3+L1 in parallel with the current source. C1 has its initial voltage from before, and L1 has its initial current from before.

So the question is, before the switch is closed, what is the voltage on C1 and the current through L1?

 

[builder_user]

The scheme for "before"?I forgot delete program' values...(

 

[builder_user]

After?

 

[gneill]

The "after" circuit looks fine. Can you tell the capacitor voltage and inductor current from the first circuit?

 

[builder_user]

The "after" circuit looks fine. Can you tell the capacitor voltage and inductor current from the first circuit?

I...know it?Or I need to find it?

 

[gneill]

I...know it?Or I need to find it?

You should be able to calculate the steady state value of the voltage on the capacitor, and the steady state current flowing through the inductor before the switch is closed.

These are going to serve as initial conditions for after the switch is closed.

 

[builder_user]

You should be able to calculate the steady state value of the voltage on the capacitor, and the steady state current flowing through the inductor before the switch is closed.

Voltage on capacitor can be the same as voltage on R2

 

[gneill]

Yes...

 

[builder_user]

Yes...

So R2 parrallel C and R1&&R2 parallel to J and to R&&L?
And I can delete C from the circuit?

 

[gneill]

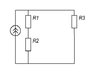
I'm not sure what your "&&" notation implies. But if you're trying to calculate the voltage on the capacitor, then notice that at steady state the capacitor "looks like" an open circuit and the inductor "looks like" a short circuit. So the current supply J will be split between the R1+R2 path and the R3 path. So it's a current divider situation.

i2 = J*R3/(R1 + R2 + R3)

 

[builder_user]

Before..?

 

[gneill]

Before..?

Yes. That's all the paths that are carrying current and making voltage drops.

 

[builder_user]

i2 = J*R3/(R1 + R2 + R3)

But R1&R2 have parallel connection with R3?

 

[gneill]

That's right. It's a current divider.

Draw a circuit with a current supply I driving two parallel resistors, Ra and Rb. How does the current divide between the Ra path and the Rb path?

The parallel resistance is Ra*Rb/(Ra+Rb). So the voltage across the pair is V = I*Ra*Rb/(Ra+Rb). Thus, the current through, say, Ra, is V/Ra, which is I*Rb/(Ra+Rb).

Now go back to your circuit. One path has resistance R1+R2, while the other has resistance R3.

 

[builder_user]

That's right. It's a current divider.

Draw a circuit with a current supply I driving two parallel resistors, Ra and Rb. How does the current divide between the Ra path and the Rb path?

The parallel resistance is Ra*Rb/(Ra+Rb). So the voltage across the pair is V = I*Ra*Rb/(Ra+Rb). Thus, the current through, say, Ra, is V/Ra, which is I*Rb/(Ra+Rb).

Now go back to your circuit. One path has resistance R1+R2, while the other has resistance R3.

A...I understand.I thought that it was voltage across all circuit.But it is voltage on R1+R2.I can find current by dividing U/R1+R2. Then I can find voltage on R2 and voltage on capacitor right?

 

[builder_user]

I found UR2.what's next?

 

[gneill]

Find the current in the inductor. You can use the same voltage divider method; it's the current through R3 this time.

 

[builder_user]

Done.What's next?

 

[gneill]

Before proceeding, let's make an educated guess at what the voltage across the inductor is going to look like when the switch closes. That way we'll know where we're headed.

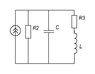
When the switch closes you'll have the current supply J = 12A in parallel with R2 and C1 and the branch R3&&L1 (using your && notation). The capacitor has an initial voltage of UC = UR2 = 9.6V (correct?). The inductor is carrying initial current iL = 9.6A (correct?).

The instant the switch closes, the capacitor will want to maintain its voltage and the inductor will want to maintain its current. So the top of R3 will be at potential UC = 9.6V. The current through R3, however, will still be iL = 9.6A, so the voltage drop on R3 is going to be 19.2V. That means the voltage across L1 must shoot up to 9.6V (- on top, + on bottom of L1) in order to satisfy Kircchoff, because UR3 + UL1 = UC at that instant.

Eventually the voltage across L1 must return to zero in a new steady state. So there will be an exponential decay (with time constant to be determined) from 9.6V down to zero. Superimposed on that will be whatever oscillations, if any, that result from the interaction of L and C. But the "big picture" is that UL1 will shoot up to 9.6V and decay.

Does all that make sense?

 

[builder_user]

Before proceeding, let's make an educated guess at what the voltage across the inductor is going to look like when the switch closes. That way we'll know where we're headed.

When the switch closes you'll have the current supply J = 12A in parallel with R2 and C1 and the branch R3&&L1 (using your && notation). The capacitor has an initial voltage of UC = UR2 = 9.6V (correct?). The inductor is carrying initial current iL = 9.6A (correct?).

The instant the switch closes, the capacitor will want to maintain its voltage and the inductor will want to maintain its current. So the top of R3 will be at potential UC = 9.6V. The current through R3, however, will still be iL = 9.6A, so the voltage drop on R3 is going to be 19.2V. That means the voltage across L1 must shoot up to 9.6V (- on top, + on bottom of L1) in order to satisfy Kircchoff, because UR3 + UL1 = UC at that instant.

Eventually the voltage across L1 must return to zero in a new steady state. So there will be an exponential decay (with time constant to be determined) from 9.6V down to zero. Superimposed on that will be whatever oscillations, if any, that result from the interaction of L and C. But the "big picture" is that UL1 will shoot up to 9.6V and decay.

Does all that make sense?

Why 12?J=4*K1=4*1.2=4.8

 

[gneill]

Isn't J = 4*K1 = 4*3 = 12? Or are the units something other than amps?

 

[builder_user]

Isn't J = 4*K1 = 4*3 = 12? Or are the units something other than amps?

But K1=1.2

 

[gneill]

Ah! My mistake. Very sorry. These K's will be the end of me...

So, make that:

iL = 3.84A
UC = 3.84V
UR3 = 7.68V
UL = 3.84V (+ on bottom end)

The general picture still stands, though, with these modified values. Do your calculated values agree, and does the argument I presented make sense?

 

[builder_user]

All values are the same

Ur3 will be iL*R3=7.68 after commutation?

 

[gneill]

All values are the same

Ur3 will be iL*R3 after commutation?

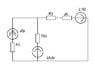
Right. The inductor maintains the same current as before the switch closes (at least for a brief instant).

So after the switch closes the circuit looks as in the attached figure, keeping in mind that C1 and L1 have their initial conditions. The idea now will be to develop the differential equations for the circuit. The current supply J and resistor R2 could be converted to a Thevenin equivalent, leaving two loops for KVL. Or you might try using a KCL approach.

A good approach might be to write the equations in differential form, convert to Laplace (allowing you to insert initial conditions), then solve for the desired variable.

 

[builder_user]

i2=i1+i3
i2*R2+Uc=E
i3*R3+Ldi/dt=0

and Uc=3.84?

But UL=-3.84?

 

[gneill]

That's fine. Keep in mind that UL and UC are initial conditions that will go into the s-domain (Laplace transformed) equations.

 

[builder_user]

I forgot Uc in my third equatation.

Why I need two previous equatations at all?
I think one will be enough
this one
i3*R3+Ldi3/dt+Uc=0

 

[gneill]

The voltage on the capacitor is not going to stay at Uc indefinitely; it's only an initial condition. If you want to find UL(t), then you'll have to solve the equations.

You should be able to notice that there are R L and C components in the circuit, so you should expect a second order system. There will be a decaying oscillation if the damping is low, or a smooth decay if the system is overdamped.

 

[builder_user]

My result

i(t)=-Uc/L+e^((-r3/L)*t)*C

Uc=3.84

I think it's wrong.

 

[builder_user]

How to do it correct?

 

[gneill]

Using whatever is your choice of circuit analysis technique you need to write out the equations for the loops (or nodes). Convert to Laplace form (s-domain) including the initial conditions, then solve.

I have not taken the time to write them out and solve them at this point, and what equations are written will depend upon your choice of analysis method. Perhaps you should post your equation attempt so that we can look at it.

 

[builder_user]

I have already posted them

I use this equatation to find i(t)
i3*R3+Ldi3/dt+Uc=0

 

[builder_user]

I've solved it correct, but It seems strange to me that equatation...System must have and i(t)=Cdu/dt and Ldi/dt

The problem is to make correct system of equatation

If I find correct equatation to solve i'll can transform it in Laplas form

At the mail problem is that I need to have my work done today

 

[gneill]

I've solved it correct, but It seems strange to me that equatation...System must have and i(t)=Cdu/dt and Ldi/dt

The problem is to make correct system of equatation

If I find correct equatation to solve i'll can transform it in Laplas form

At the mail problem is that I need to have my work done today

Well, I'm glad that you've solved it. Congratulations.

I don't find it surprising that the equations will involve changing values on both the capacitor and inductor; it's a second order system, and the configuration is capable of producing oscillations (ringing) or other "excursions" when its perturbed (like the throwing of the switch does). The precise response depends upon the component values (damping).

 

[builder_user]

I make new equatation and solve for transformed scheme
J2=(J*1/sC+L*i0-U/s)/(R3+s*L+1/s*C)
Here my result.Is it correct now?
i(t)=(1.9-34464*j)*e^((-1428+1421j)*t)+(34464-1.9j)*e^((-1428-14211*j)*t)*i
u(t)=L*di/dt=(342835-34469*j)*e^((-1428+14211)*jt)+(342835+34469*j)*e^(-1428+14211j)t

 

[gneill]

I'm not understanding how you arrived at your equation for J2 (is that the current for the inductor?). There are two loops so there should be two loop equations. In your figure, is J/p meant to be a current source in series with resistor R2? How did you get from the original circuit with a current source in parallel with Rs to one with it in series? I see that you've drawn in the s-domain sources associated with the initial conditions. That's good.

If I plug t = 0 into your u(t) solution the answer I see looks a bit large. Is it scaled somehow?

 

[builder_user]

I'm not understanding how you arrived at your equation for J2 (is that the current for the inductor?). There are two loops so there should be two loop equations.

But there is only one variable.---J2(on resistor R3).Besides if I make 2 equatations Mathcad can't find J2