gneill
Mentor
- 20,989
- 2,934
Before proceeding, let's make an educated guess at what the voltage across the inductor is going to look like when the switch closes. That way we'll know where we're headed.
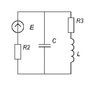
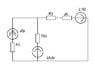
When the switch closes you'll have the current supply J = 12A in parallel with R2 and C1 and the branch R3&&L1 (using your && notation). The capacitor has an initial voltage of UC = UR2 = 9.6V (correct?). The inductor is carrying initial current iL = 9.6A (correct?).
The instant the switch closes, the capacitor will want to maintain its voltage and the inductor will want to maintain its current. So the top of R3 will be at potential UC = 9.6V. The current through R3, however, will still be iL = 9.6A, so the voltage drop on R3 is going to be 19.2V. That means the voltage across L1 must shoot up to 9.6V (- on top, + on bottom of L1) in order to satisfy Kircchoff, because UR3 + UL1 = UC at that instant.
Eventually the voltage across L1 must return to zero in a new steady state. So there will be an exponential decay (with time constant to be determined) from 9.6V down to zero. Superimposed on that will be whatever oscillations, if any, that result from the interaction of L and C. But the "big picture" is that UL1 will shoot up to 9.6V and decay.
Does all that make sense?