What is the instantaneous value of UL after commutation?

[builder_user]

Ok.So I just need to make system of equatations and only to solve it?

 

[gneill]

so, for L i'll just need to use U=Ldi/dt?

Essentially, yes. The transition that occurs when the switch is closed will be the same as applying a step change in the source current. Or if you wish, it will be equivalent to applying a voltage source to an RL circuit.

 

[gneill]

Ok.So I just need to make system of equatations and only to solve it?

If that is your goal, sure. And it will be one differential equation; The one for a parallel RL circuit driven by a current source.

 

[gneill]

Perhaps I should summarize the work done so far. The equivalent circuits for before the switch is closed and after the switch is closed are as in the attached image. These are simple circuits!

To analyze the instant of switch closure, you can produce a "differential" circuit that reflects the change between the two. The difference is the sudden change in current and change in parallel resistance. Since you are looking for the voltage across the inductor after the switch closes, the circuit to write the equation for will consist of a current supply with a value equal to the change in current, the parallel resistance of the "after switch closed" circuit, and the inductor.

 

[builder_user]

Final part.At the moment of commutation scheme(pic.)

It has only one equatation?

(Req+R3+R4)*i+Ldi/dt=J*Req

and I must find i??

How to do it in Mathcad?

 

[builder_user]

I've found i(t)=1.43+1.06*e^-1567t

To find U i only need to
U=i(t)'*L?

U(t)=-19.93*e^(-1567t)

Is it correct?About Laplace.
In what state I need to replace inductor with pL.before commutation and after commutation I do not have inductor.Does it mean that I only need to replace inductor at the moment of commutation?

 

[builder_user]

After operator method results are different

i(t)=1.43+1.06*e^-1567t vs i(t)=1.43-0.0000915*e^-1563t

 

[gneill]

I've found i(t)=1.43+1.06*e^-1567t

To find U i only need to
U=i(t)'*L?

U(t)=-19.93*e^(-1567t)

Is it correct?


About Laplace.
In what state I need to replace inductor with pL.before commutation and after commutation I do not have inductor.Does it mean that I only need to replace inductor at the moment of commutation?

Hi builder-user, sorry to be away so long...

Your equations look fine except the time constant parameter seems to be missing a decimal place; I see R/L as 1.567 given your component values.

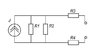
My own method when I solve these sorts of problems where there's a sudden transition involved (like the switch being closed), is to find the equivalent circuits for before and after steady state conditions, then produce a "difference" circuit to analyze. The difference circuit incorporates the final steady state circuit components, and where the source is the change in source between the old and new states. So in this case, looking at the Norton equivalents, the "old" current source was 2.49, the "new" source was 1.43, so the change in source is -1.06. See the attached figure. I then analyze this circuit assuming no prior state ("power-on" is at t=0).

The results of this analysis will be the changes that will occur in the original circuit after the switch closes. It will give the voltage across the inductor, and the change in current through the inductor. So if the pre-switching steady state current through the inductor was I₀, and the analysis provided current I₁(t), then we have I(t) = I₀ + I₁(t) for when the switch is closed.

This method may or may not suit you.

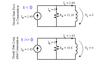
To incorporate the initial inductor current into the Laplace transform method, it appears as an initial condition for the current -- the i_o term in L*(s*I - i_o).

So if you have the Thevenin equivalent of the circuit at time t = 0 (when the switch has just been closed), with voltage source V and series resistance R and series inductor L, the equation you write for the Laplace transform of the current looks like:

V/s = I*R + L*(s*I - i₀)

Solve for I, take the inverse Laplace transform, and you're done (for the current, at least).

 

[builder_user]

Your equations look fine except the time constant parameter seems to be missing a decimal place; I see R/L as 1.567 given your component values.

You mean 1.43+1.06*e^-1.567t?

So if you have the Thevenin equivalent of the circuit at time t = 0

At time t=0 I need to add inductor to all resistance?And where is the potensial difference?

 

[gneill]

You mean 1.43+1.06*e^-1.567t?

Yes. I'm taking the component values as:

R1 = 5.6
R2 = 5.6
R3 = 4
R4 = 12
L = 12

Those are what I get after applying your 'K' constants.

These yield a Thevenin resistance of 18.8 when the switch is closed. So the time constant for the circuit should be τ = 12/18.8 = 0.6383, and 1/τ is 1.567

At time t=0 I need to add inductor to all resistance?And where is the potensial difference?

I not sure that I understand what you're asking. If you're referring to the Laplace transform equation, then I started with the Thevenin equivalent circuit and wrote KVL around the loop. The V is the Thevenin source voltage. i₀ is the initial current flowing in the inductor at t=0 when the switch is closed.

V = i*R + L*di/dt

Laplace transform:

V/s = R*I + L*(s*I - i₀)

I = (V + L*i₀*s)/(L*s² + s*R)

inverse Laplace transform:

i(t) = (i₀ - V/R)e(-R*t/L) + V/R

 

[builder_user]

l = 12

l=0.012

 

[gneill]

l=0.012

If you say so. In your first post you had:

K1=1.2
L = 10*K1

You did not indicate units (for anything!) so I assumed Ohms for resistances and Henries for inductance.

 

[builder_user]

Thevenin equivalent circuit and wrote KVL around the loop.

This loop?

 

[builder_user]

You did not indicate units (for anything!) so I assumed Ohms for resistances and Henries for inductance.

I forgot.In every task I have millihenries and so I've not written it there.

 

[gneill]

This loop?

No, this loop. All of the source and resistor network is replaced by its Thevenin equivalent. Makes life simple.

 

[gneill]

I forgot.In every task I have millihenries and so I've not written it there.

Okay. Perhaps in future you should just state the component values. All the K multipliers and assumed units is confusing.

 

[builder_user]

No, this loop. All of the source and resistor network is replaced by its Thevenin equivalent. Makes life simple.

Thevenin equivalent after commutation?Or at the moment of commutation?One of the equivalents that was found before?Or not found in this topic?

 

[gneill]

Thevenin equivalent after commutation?Or at the moment of commutation?One of the equivalents that was found before?Or not found in this topic?

After the switch closes, so yes, after commutation.

The circuit at the moment the switch closes remains the same thereafter.

It's only the initial conditions (the existing current in the inductor) that makes the moment of commutation special.

 

[builder_user]

How to do inverse Laplace transform in MathCAD?

 

[gneill]

How to do inverse Laplace transform in MathCAD?

Select the 's' variable and then Symbolics --> Transform --> Inverse Laplace.

 

[builder_user]

Thanks.