Dante Tufano
- 32
- 0
Okay, so here's the question:
The figure below shows the kinetic energy K of a simple pendulum versus its angle θ from the vertical. The pendulum bob has mass 0.320 kg. What is the length of the pendulum?
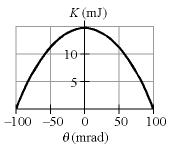
Equations: KE=(mv^2)/2
U=mgh
x(t)=xmcos(wt+phi)
I solved for the height by setting the max kinetic energy equal to the max potential energy, and got .004783, but I have no idea how to use the position equation to find the max velocity or what to do after that. Could I please get some guidance?
The figure below shows the kinetic energy K of a simple pendulum versus its angle θ from the vertical. The pendulum bob has mass 0.320 kg. What is the length of the pendulum?
Equations: KE=(mv^2)/2
U=mgh
x(t)=xmcos(wt+phi)
I solved for the height by setting the max kinetic energy equal to the max potential energy, and got .004783, but I have no idea how to use the position equation to find the max velocity or what to do after that. Could I please get some guidance?