Their answer is incorrect, at least as regards the minimum. What they give is a lower bound, not a best lower bound.
Your original message did not mention that angles were to be ≤ π/2; that changes things a lot!
So, let us look at two possible versions of the problem (with ##f(x) \equiv \sin(x)/x##).
(I) The unrestricted-angle problem:
\min F = f(A) + f(B) + f(C)\\<br />
\text{subject to}\\<br />
A+B+C=\pi\\<br />
A,B,C \geq 0
(II) The restricted-angle problem:
\min F = f(A) + f(B) + f(C)\\<br />
\text{subject to}\\<br />
A + B + C = \pi\\<br />
0 \leq A,B,C \leq \pi/2
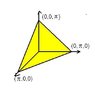
There are three solutions of (I): (A,B,C) = (π,0,0) or (0,π,0) or (0,0,π). These all give F = 2, which is strictly larger than your textbook's lower bound of 6/π = 1.909859317. As I said before, these three solutions do not correspond to actual triangles; they are 'degenerate' triangles that have been collapsed down to a line segment. However, for any F > 2 you can find actual triangles giving that value of F.
There are three solutions of (II): (A,B,C) = (π/2,π/2,0) or (π/2,0,π/2) or (0,π/2,π/2), all giving F = 1 + 4/π = 2.273239544. Again, these do not correspond to any real triangles, because no real triangle can have two 90-degree internal angles. However, we can find real triangles that give any value > 1 + 4/π. For example, the triangle with corners (0,0), (1,0) and (0,n) in the Cartesian plane will have internal angles π/2, arctan(n) and arctan(1/n). For very large finite n we have nearly (but not quite) two right angles; in the limit n → ∞ we get our 'solution'.