Finding Maximum Altitude of a Rocket

[stupif]

1. a rocket is launched from rest and moves in a straight line at 70degree above the horizontal with an acceleration of 46ms^(-2) . After 30seconds of powered flight , the engines shut off and the rocket follows a parabolic path back to earth. find
1)the maximun altitude reached


2. i use this formula, s= ut +1/2at^2
s=? , u=0, t= 30, a= (46-9.81 )
the correct answer is 105.16km, i didt get the answer~


3. why can't get the answer and how should i do to get correct answer?
　　　ｈｅｌｐ　ｍｅ．．．ｔｈａｎｋ　ｙｏｕ

 

[gneill]

During the powered portion of the flight you are given the rocket's angle and acceleration, and told that the trajectory is a straight line. So at the end of the powered portion (20 seconds duration) what is the speed of the rocket and its height? How about the vertical component of its speed?

 

[stupif]

use which one formula?

 

[gneill]

use which one formula?

For speed, use a formula that includes acceleration and time and gives velocity.

For distance, use a formula that includes acceleration and time and gives distance

What formulas do you know?

 

[stupif]

i know this formula, v= u + at
s= ut +1/2at^2, correct?

 

[gneill]

i know this formula, v= u + at
s= ut +1/2at^2, correct?

Yes, fine. Which one will give you the speed of the rocket, traveling in a straight line with acceleration a=46ms^-2 for 30 seconds?

 

[stupif]

1380m/s??
after that?
i use this formula s=ut+1/2 at^2 to find distance
u= 0, t=30 a=46, correct?

 

[gneill]

1380m/s??
after that?
i use this formula s=ut+1/2 at^2 to find distance
u= 0, t=30 a=46, correct?

Yes, fine so far. Determine the height of the rocket at burnout from its distance traveled (it's been traveling at a 70° angle, remember). From the speed and angle, determine the vertical component of the velocity. Then treat these circumstances as a new projectile problem for the unpowered portion of the flight.

 

[stupif]

s=ut +1/2 at^2
s= 1380sin 70(30)+ 1/2 (46)(30)^2
my answer is 59.603km
but answer is 105.16km

 

[gneill]

s=ut +1/2 at^2
s= 1380sin 70(30)+ 1/2 (46)(30)^2
my answer is 59.603km
but answer is 105.16km

Your speed, 1380m/s is at the *end* of the 30 second burn. It is not the initial velocity of the rocket (that's zero).

You are currently looking for the height of the rocket when its fuel runs out (after 30 seconds). What is that height?

 

[stupif]

then using wat formula?

 

[gneill]

Using the formula that gives you distance when you know the acceleration and time.

 

[stupif]

v = u + 2as, v=0, u=1380m/s ,a= 46

this formula?

 

[gneill]

Nope. Use s = (1/2)at²

You can either calculate the distance along the straight trajectory and then find the vertical height at the end using the trajectory's angle with the horizontal, or you can calculate the height directly by using in the formula only the vertical component of the acceleration.

 

[stupif]

sorry...you are confusing me...

 

[gneill]

sorry...you are confusing me...

Let's see if we can fix that

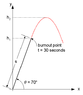
Attached is a diagram of the rocket trajectory. It's a straight line until the fuel runs out after 30 seconds, at which point it will have traveled some distance s along the trajectory and reached height h₁ with some speed v. This speed will be directed along the trajectory (angle 70° to the horizontal).

After burnout the rocket is just a projectile with a ballistic (unpowered) trajectory. It's a parabolic trajectory.

So there are two sections of the trajectory to worry about. First the powered section, which you are told is a straight line with a given acceleration, and the second is a simple projectile motion with an initial velocity and height and launch angle (70°).

The first order of business is to find out where the rocket is at the end of the powered section, and how fast it is traveling. Those will in fact be the initial conditions for the second section of the trajectory. The distance it travels in that first section is designated s in the figure. The height it achieves is h₁.

Now, to find the height of the rocket you can either find s using the given acceleration along the straight line for the specified time (30 seconds) and then use trig to find the vertical distance from that, or you can realize that the acceleration has both vertical and horizontal components and use the vertical component of acceleration to find that height. In either case the formula to use is (1/2)at². In the first case the acceleration is a=46m/s², directed along the trajectory. In the second case it's the vertical component of a (use the angle and trig to break the 46m/s² into its vertical and horizontal components).

Does that help?

 

[stupif]

now, i really understand the question, you are too great.
thank you.
but how to find h2,
i use this formula, v=u +2as
u=1380m/s, a=9.8, v=0

 

[I like Serena]

Let's see if we can fix that

Woooooooooooooooowwwww!

 

[stupif]

now, i really understand. you are too great. thank you very much
but now h2 how to find?
i use this equation v= u +2as
v= 0, u= 1380 a=9.8

 

[gneill]

now, i really understand. you are too great. thank you very much
but now h2 how to find?
i use this equation v= u +2as
v= 0, u= 1380 a=9.8

First, let's make sure that you've got the first height. What did you get for h₁?

 

[andorrak]

when I was learning this stuff, you just got to grasp your head around the x speed always staying constant with only the y speed changing.

 

[stupif]

my h1 is 20700m

 

[gneill]

my h1 is 20700m

That seems just a bit too big. It looks like it might be the distance s, measured along the straight line trajectory, rather than the height h₁, which is the vertical component. Can you show your calculation?

 

[stupif]

s= ut + 1/2 at^2
= 0(30) +1/2 (46)(30)^2

 

[gneill]

s= ut + 1/2 at^2
= 0(30) +1/2 (46)(30)^2

As I surmised, that calculation gives you the length of the straight line trajectory, s in the diagram that I made, rather than the height. This distance forms the hypotenuse of a triangle which has the height h₁ as one side and the horizontal distance traveled as the other. You should be able to calculate h₁ using s and the angle that s makes with the horizontal.

 

[stupif]

20700 sin 70??

 

[gneill]

20700 sin 70??

Yes. That will be the height h₁ where the powered part of the trajectory ends (at t = 30 seconds) and the free-fall part of the trajectory begins. Make a note of that value.

Now let's turn to the second portion of the trajectory. The rocket, with its fuel gone, is now a simple projectile. It has an initial speed, height, and launch angle, and you want to find the highest elevation achieved. What approach will you take? (Do you know of more than one?)

(Remember that the rocket's velocity will have both vertical and horizontal components, and that the speed you calculated previously is the speed in the direction of the straight-line portion of the trajectory -- it's the magnitude of the velocity vector).

 

[stupif]

speed is 1380sin70 + 1380cos70 =1768.76m/s
then i v^2 = u^2 +2 as, 0=1768.76^2 +2(9.8)s
s= 159617.96m.
correct?

 

[gneill]

speed is 1380sin70 + 1380cos70 =1768.76m/s
then i v^2 = u^2 +2 as, 0=1768.76^2 +2(9.8)s
s= 159617.96m.
correct?

Well... You want to use just the vertical component of the velocity, 1380sin70. That's the only part of the velocity vector that's acting to change the height of the rocket.

Also, linearly adding the magnitudes of the vertical and horizontal components of a vector together doesn't yield a meaningful quantity. Vector components "add in quadrature", which, translated into plainer terms means that they add like the sides of a right angle triangle "add" to yield the hypotenuse: v = \sqrt{v_y^2 + v_x^2}. Here v is your speed, 1380 m/s, and v_y and v_x are the vertical and horizontal components of that speed.

 

[stupif]

i don't understand~

 

[gneill]

Have you studied projectile motion, where the horizontal and vertical components of the motion are treated independently?

The velocity vector for a projectile, at any given instant, is made up of two components: a vertical component and a horizontal component. Only the vertical component of the motion is important for calculating the height of the projectile at any time.

In calculating the height of the rocket projectile, you want to concern yourself only with the vertical component of the velocity. That is the 1380*sin(70°) value.

 

[stupif]

ya...i have studied.
what i know in projectile motion is vetical velocity in changing because of the gravity,use this formula, s=ut +1/2 at^2,
the horizontal velocity is constant because of the inertia , so use s=vt

so, 1380sin 70 = 1296.78
after that, what should i do?

 

[gneill]

ya...i have studied.
what i know in projectile motion is vetical velocity in changing because of the gravity,use this formula, s=ut +1/2 at^2,
the horizontal velocity is constant because of the inertia , so use s=vt

so, 1380sin 70 = 1296.78
after that, what should i do?

1296.78 m/s is the "u" in your u*t + 1/2 at² formula. It's the initial vertical velocity at the beginning of the free-fall portion of the rocket's trajectory.

But you want to find the maximum height. So you might want to choose another formula to use with this velocity. Previously you wrote the equation, v_f² = v_i² + 2*a*d. Here the initial velocity, v_i, would be your u.

 

[stupif]

so is 19451.64m + 85797.88= 105249.52m
but the answer is 105.6km. a slightly differences. is it correct??

 

[gneill]

so is 19451.64m + 85797.88= 105249.52m
but the answer is 105.6km. a slightly differences. is it correct??

The difference is probably due to the use of slightly difference value for g, the acceleration due to gravity. But yes, the value looks okay.

 

[stupif]

okay~thank you very much. now the next question is the time of flight from launching to impact...answer is 308.65s
i don't know what the question talking about?
what is the impact it means?

 

[gneill]

okay~thank you very much. now the next question is the time of flight from launching to impact...answer is 308.65s
i don't know what the question talking about?
what is the impact it means?

Presumably that would be when the rocket crash-lands on the ground. After the fuel was used up the rocket became a free-falling projectile. It will rise to its maximum height and then fall back to the ground.

 

[stupif]

thanks, i got it, now the next question is the distance from launched pad to impact point.
the answer is 139km

1st i find the distance at s1, 20700cos 70 = 7029.82m
2nd, i find the distance between s1 and s2 , s=vt, s= 1380cos70 X 28.19s = 13305m
3rd, i find the distance between s2 to the ground, s=vt , s= 1380cos70 X 146.50s =69146m

total up is 89480.82m

i think something wrong in step 2 and 3.

 

[gneill]

It's difficult to comment without knowing where the numbers and constants are coming from. What are s1 and s2? Where do the time intervals 28.19s and 146.50s come from?

 

[stupif]

s1 is the distance from rest to h1
s2 is the distance from h1 to h2 when the engines shut off

mistake for 28.19. it should 30s
146.50 is come from this equation, s = ut +1/2at^2 , 105.16km= 0t+ 1/2(9.8)t^2
t= 146. 50s

 

[gneill]

s1 is the distance from rest to h1
s2 is the distance from h1 to h2 when the engines shut off

mistake for 28.19. it should 30s
146.50 is come from this equation, s = ut +1/2at^2 , 105.16km= 0t+ 1/2(9.8)t^2
t= 146. 50s

It looks as though your s1 and s2 values are horizontal distances, with s1 being the the horizontal distance from launch to where the fuel runs out, and s2 the horizontal distance from there to the maximum height.

Why do you take the time between s1 and s2 to be 30 seconds?

 

[stupif]

sorry...mistake again...i know how to do already, just now made some mistakes in calculation.
thank you very much...