utkarshakash
Gold Member
- 852
- 13
Homework Statement
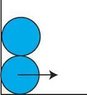
Two identical uniform cylinders of radius R each are placed on top of each other next to a wall as shown. After a disturbance, the bottom cylinder slightly moves to the right and the system comes into motion. Find the maximum subsequent speed of the bottom cylinder. Neglect friction between all surfaces.
See attachment for diagram
The Attempt at a Solution
Let the final speed of the lower and upper cylinders be vb and vu respectively and their angular velocity be ωb and ωu.
Conserving energy
3mgR + mgR=\dfrac{mv_b ^2}{2} + \dfrac{mv_u ^2}{2}+\dfrac{mv_b ^2}{4}+\dfrac{mv_u ^2}{4} + 2mgR \\<br /> v_b ^2 + v_u ^2=\dfrac{8gr}{3}
I have assumed that the cylinders do not slip on the surface and perform pure rolling. I need another equation as there are two variables.