Finding Minimum Friction for Static Wedge: A Free Body Analysis Approach

  • Thread starter Thread starter safat
  • Start date Start date
  • Tags Tags
    Friction Plane
AI Thread Summary
To determine the minimum coefficient of friction (μ) required for a static wedge to remain stationary, a free body analysis is essential. The discussion emphasizes identifying all forces acting on the wedge, including tension forces F1 and F2. It clarifies that the wedge has mass M and a smooth surface, indicating no friction between the wedge and block M1. Participants suggest conducting a thorough analysis of the forces and accelerations while assuming the wedge is stationary. The goal is to accurately calculate the forces exerted by tension on the wedge to find the necessary friction coefficient.
safat
Messages
14
Reaction score
0

Homework Statement


Find the minimum μ required between wedge M and ground so that it stays static.


Homework Equations



I already found the equations for accelerations and tension (when μ is big).
Do I need them?

The Attempt at a Solution


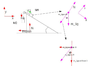
I would like to know whether I found all the forces acting on the wedge. (see attachment)
Which component should I use for the green arrow force?
NB the red forces act on the wedge
 

Attachments

  • Screenshot from 2013-03-11 20:31:41.png
    Screenshot from 2013-03-11 20:31:41.png
    31.3 KB · Views: 436
Last edited:
Physics news on Phys.org
Is the wedge massless? Is there friction between the wedge and M1?
 
no, wedge has mas M, and its surface it's smooth.
 
F1 and F2 are the tension, yes?
 
I think so.
 
Go through the usual free body analysis on the two blocks (assuming the wedge is stationary) to find the acceleration and the tension. Then figure out the forces the tension applies to the wedge.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Find min/max accel. for block to stay on wedge (static fric)
Replies
1
Views
2K
Is it friction or tension acting on the person hanging on a rope?
Replies
4
Views
1K
How to Calculate Reversed Force of a Wedge | Friction and Wedges Homework
Replies
9
Views
7K
Acceleration of a block on a moving wedge
Replies
6
Views
3K
Finding the work done by a block
Replies
4
Views
3K
What is the Minimum Coefficient of Static Friction to Keep the Wedge Stationary?
Replies
9
Views
2K
Why is the direction of kinetic/static friction up a ramp?
Replies
7
Views
1K
How can I determine the instant the block overcomes static friction?
2
Replies
61
Views
3K
Finding angle required for equilibrium on a slope
Replies
12
Views
3K
Maximizing Friction Coefficient for Block on a Wedge: A Calculus Approach
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top