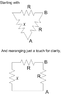- #1
physicsforus
- 6
- 0
Homework Statement
What is the resistance of the (semi-)infinite resistor chain below, between points A and B, if R = 25 ohms?
The Attempt at a Solution
I am not sure where to begin exactly, but I am thinking of this formula:
VAB=VB-VA=∑ε-∑i.R
or
[PLAIN]https://www.physicsforums.com/latex_images/12/1284517-1.png
Just not quite for sure.
Last edited by a moderator: