Finding stress in non symetric cross section

[Dell]

in a given shaft with a circular cross section, the radius changes linearly

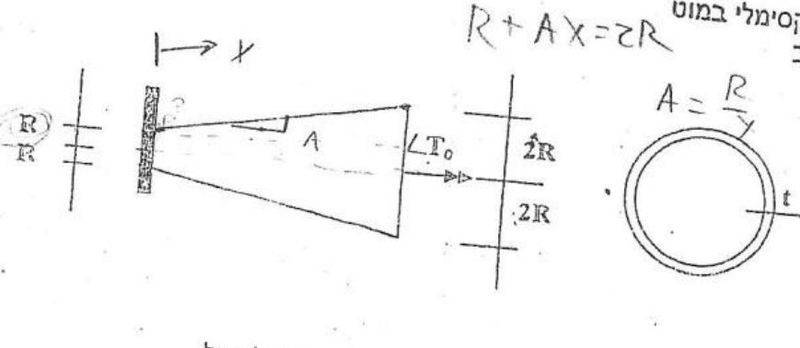
find the maximum shear stress

i used T*r/J
and since J is dependant on r^4, i found that the cross section with the smallest radius will feel the largest stress.

find the angle of twist at the end of the shaft

T/(GJ)*dx while J is a function of X and i integrate from 0 to L

if the bottom of the shaft is reinforced, -thickened- to 2t, what is the largest shear stress felt in the shaft??

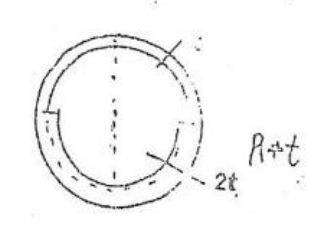
up till now i have only solved questions with either circular/ rectangular closed cross sections, or other open cross sections

can i use the equation for maximum stress
T/(2A*t)

where A is the area surrounded by an axis through the center of the side of the shape?? if so how do i do this ? what would that axis look like? would it be 2 half circles with 90 degree joints? meaning the area would be pi/2*(R1²+R2²) where R1 and R2 are the average radii of the 2 half circles??

using this logic i would find the maximum stress in the thin walled circle

is this correct? can i do this?

this is where i am stumped,

 

[Dell]

also what are the advantages of thickening parts of the shaft, i think if it was subjected to bending this might improve its performance as far as max moment that can be applied, but in torsion what would this do? there any other advantagees?