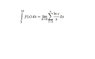phillyolly
- 157
- 0
Homework Statement
Use Definition 2 to find an expression for the area under the graph of f as a limit. Do not evaluate the limit
f(x)=(lnx)/x
3 ≤ x ≤ 10
Homework Equations
See the attachment for the Definition 2.
The Attempt at a Solution
∫ ln(x) / x dx = 1/2 (ln(x))² + C
10
∫ ln(x) / x dx = 1/2 [ (ln(10))² - (ln(3))² ]
3