Finding the Center of Mass of a Uniform Disc: A Non-Calculus Approach

AI Thread Summary
The discussion focuses on finding the center of mass of one-fourth of a uniform disc without using calculus. A member expresses difficulty in solving the problem, which involves understanding the shift in the center of mass when a full circle is folded in half. Another participant suggests considering symmetry as a key approach to the solution. The hint provided helps the original poster make progress in solving the problem. The conversation emphasizes the importance of geometric reasoning in physics problems.
Ujjawal Kumar
Messages
2
Reaction score
0
Hi New member here!
1. Homework Statement

In the figure one-fourth part of a uniform disc of radius R is shown. The distance of the center of mass of this object from center ‘O’ is ……………………….
PictureR.png


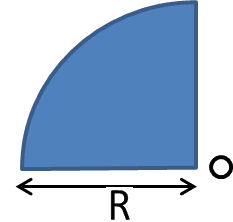
Given: For a semi-circular disc with origin of co- ordinate system at the center of circle, the coordinate of its center of mass is (0,4R/3π ).

(Solve this problem without using calculus)

The Attempt at a Solution


I tried for hours but could not find a solution without using calculus.
 
Last edited:
Physics news on Phys.org
Hello Ujjawal, welcome to PF :smile: !

A challenging exercise. Think symmetry and folding:
The given information tells you the center of mass shifts from 0 to ##(0,{4\pi \over 3r})## when you fold a full circle in half.

Is that enough of a hint ?
 
  • Like
Likes Ujjawal Kumar and SammyS
Yes, and thank you BvU!
 
This problem actually took me quite some time to figure...thnx for the hint BvU!
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Finding Mass Center of a Circular Disc with Hole & Weight
Replies
3
Views
2K
Finding the center of mass of a simple 2D shape
Replies
9
Views
3K
How Does External Force Affect a Rotating Disc and Ring System?
Replies
6
Views
3K
How to find centroid of a hemisphere using Pappus's centroid theorem?
Replies
27
Views
4K
Finding Center of Mass of Disc with Hole
Replies
12
Views
2K
Finding the center of mass of a homogeneous object
Replies
6
Views
4K
Moment of Inertia of a Spinning Record with a Hole in Center
Replies
13
Views
4K
Rotation of Rigid Bodies: Rotating stick with disc on top
Replies
9
Views
2K
How Does Impulse Affect Acceleration and Tension in a Disk-Particle System?
Replies
30
Views
5K
Finding the Total Charge of a Non-Uniformly Charged Disc
Replies
5
Views
1K

Hot Threads

Recent Insights

Back
Top