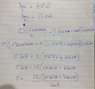Neolightdraco
- 2
- 0
Homework Statement
Using Gauss law,
Since there has been no mention of which type of charge density we have to find out I assumed it to be surface charge density since Gauss Law is in surface intergration , and I don't think there is any need to doing integration since the options given are results obtained without integration , I just can't get what's wrong
Is the problem in my choice of charge density or my method of solving it wrong?