oomba
- 2
- 0
Hello
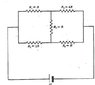
**attachment of problem diagram at bottom**
1)Find the current through R3
2) Find the total equivalent resistance of the circuit
Ohm's law, parallel resistances, series resistances, Thevenin's theorem, and all that jazz
Okay, for #1, I actually got already. I thought the easiest way to do it would be to utilize Thevenin's equivalent method. So I was able to reduce the circuit down to just the thevenin "load" voltage (which I computed as (7E/15), the thevenin resistance (which I got (22R/15) for, and the load resistor R3. I found the current through R3 to be (7E)/(37R) and I'm pretty sure that's correct.
The real problem is with finding the equivalent resistance of those 5 resistors. I don't see any easily attainable series/parallel resistor combinations thanks to that middle wire with the resistance on it, unless I'm overlooking something pretty badly. Being that there are no numbers given in this problem, what type of approach should I attempt to find Req of that entire branch?
If you can't see the pic, it's basically a closed, looped rectangle located between the terminals of the battery. The rectangle is divided into 2 squares by a wire with a resistance on it, where there are 2 resistors "in a parallel configuration" with each other on both squares.
Homework Statement
**attachment of problem diagram at bottom**
1)Find the current through R3
2) Find the total equivalent resistance of the circuit
Homework Equations
Ohm's law, parallel resistances, series resistances, Thevenin's theorem, and all that jazz
The Attempt at a Solution
Okay, for #1, I actually got already. I thought the easiest way to do it would be to utilize Thevenin's equivalent method. So I was able to reduce the circuit down to just the thevenin "load" voltage (which I computed as (7E/15), the thevenin resistance (which I got (22R/15) for, and the load resistor R3. I found the current through R3 to be (7E)/(37R) and I'm pretty sure that's correct.
The real problem is with finding the equivalent resistance of those 5 resistors. I don't see any easily attainable series/parallel resistor combinations thanks to that middle wire with the resistance on it, unless I'm overlooking something pretty badly. Being that there are no numbers given in this problem, what type of approach should I attempt to find Req of that entire branch?
If you can't see the pic, it's basically a closed, looped rectangle located between the terminals of the battery. The rectangle is divided into 2 squares by a wire with a resistance on it, where there are 2 resistors "in a parallel configuration" with each other on both squares.