paulmdrdo
- 89
- 2
Summary:: I was trying to derive the equation for the output impedance of the ICIS circuit.
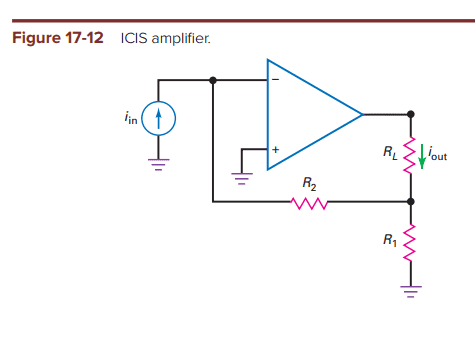
Here's what I've tried so far.
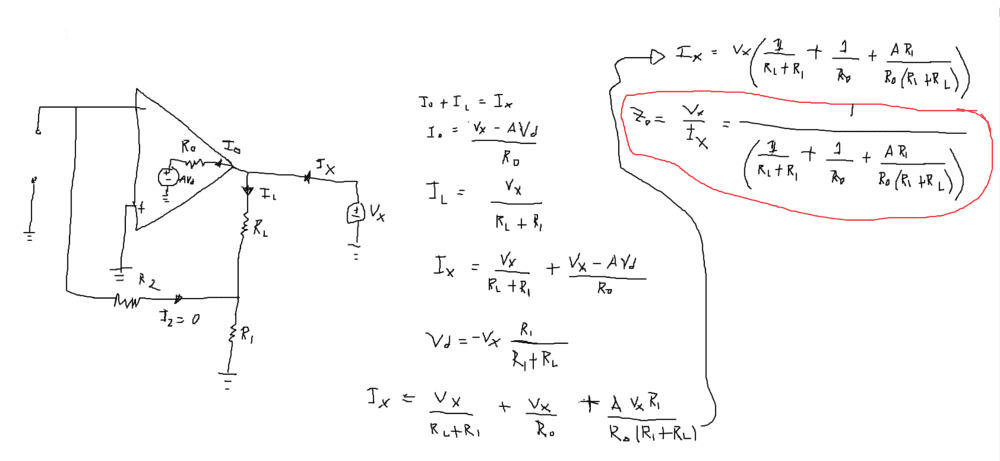
What I have derived does not agree with the one provided in my book.
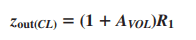
Since it is a current source the negative feedback must increase the output impedance. The one I derived says otherwise. Can you tell me what I am missing? TIA!
Here's what I've tried so far.
What I have derived does not agree with the one provided in my book.
Since it is a current source the negative feedback must increase the output impedance. The one I derived says otherwise. Can you tell me what I am missing? TIA!