Finding the tension on lifting chains

[ted potts]

Hi folks, I'm a construction worker helping to destruct an oil platform out in the north sea, I often have to work out weights applied on lifting slings during cross hauling scenarios like the one drawn here, I know 2 ways of working this out already; 1 using a calculation of all the triangles lengths and another by drawing a triangle having one side representing the load ie,1000kg = 10 cm and then drawing the rigging angle side which should represent the tension... however, I'm sure there's a way of calculating this using the angles, cos and sin ... I've had a play but can't get my head round it, can anyone help me with this by explaining the equation please? ps I am not all the best with mathematical symbols so if you could explain it as I would enter it into the calculator id appreciate it, Thanks Ted

 

[HallsofIvy]

Let the tension in the left chain (with the 44, 46 degree angles) be T_1 and the tension in the right chain (with the 34, 36 degree angle) be T_2.. The horizontal component of force in the left chain is T_1 cos(44) and the vertical component is T_1 sin(44). Similarly the horizontal component of force in the right chain is T_2 cos(56) and the vertical component is T_2 sin(56). The total of the vertical components is the weight being lifted, T_1 sin(44)+ T_2 sin(56)= 1000g and, in order that the weight not move left or right, the horizontal components must cancel, T_1 cos(44)= T_2 cos(56). Solve those two equations for T_1 and T_2.

 

[BvU]

Hello Ted,

I feel a heavy responsibility to explain this right and without possibility of misunderstanding ! Wouldn't want to be responsible for your weight dropping into the North sea and even less for denting a hole in a ship or whatever underneath .

Doing calculations on the static situation is the first stage: you assume load forces are only due to gravity, not to acceleration (i.e. you lift very slowly and smoothly ... ahem..)

And you make use of Newton's law: the load hangs still if the sum of forces on the thing is zero $\sum\vec F = 0$

Therefore you make a so-called free body diagram (or here) of the forces on the load.

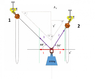
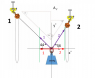
Forces in your example are gravity and two sling tensions. Forces are vectors, hence the appearance of these sines and cosines. Vectors have components and the easiest is to look at horizontal and vertical components. Since gravity is vertical, the only horizontal components are from the two sling tensions. So if the sum of horizontal forces has to be zero, these two slings have to pull equally hard in opposite directions in the horizontal plane. In words: red 1 = red 2. In your picture:

And in a formula : $$ \begin {equation} T_1 \cos(44^\circ) = T_2 \cos (56^\circ) \label {eq:F_hor} \end {equation} $$
------------------------------------------------------------------------------------------------------------

In the vertical direction the two slings pull upwards and gravity pulls down. Together the two slings' vertical components have to compensate the weight. In words: blue 1 + blue 2 = 1000 kg * g. In your picture:

and in a formula: $$ \begin {equation} T_1 \sin(44^\circ) + T_2 \sin (56^\circ) = 1000 {\rm \ kg\;} \times g\label {eq:F_vert} \end {equation} $$

[edit] sorry, pressed post reply too quickly. Will continue later.

 

[BvU]

OK, back to business: we had (and I'm glad to have found Ivy come up with the same):
$$\begin {equation} T_1 \cos(44^\circ) = T_2 \cos (56^\circ) \label {eq:F_hor2} \end {equation}$$ $$\begin {equation} T_1 \sin(44^\circ) + T_2 \sin (56^\circ) = 1000 {\rm \ kg\;} \times g\label {eq:F_vrt2} \end {equation}$$ and we are ready to develop a solution algorithm. I don't know the particulars of you calculator, so I'm afraid some further translation step may be needed later on...
From $\eqref {eq:F_hor2}$ :$$\begin {equation} T_2 = T_1 \; { \cos(44^\circ) \over \cos (56^\circ) } \label {eq:T2} \end {equation}$$ and we rewrite $\eqref {eq:F_vrt2}$ using this $\eqref {eq:T2}$ to get $$
\begin {equation} T_1 \sin(44^\circ) + T_1 \; \cos(44^\circ) \; {\sin (56^\circ) \over \cos (56^\circ) } = 1000 {\rm \ kg\;} \times g\label {eq:T1} \quad \Rightarrow \end {equation} $$ $$
\begin {equation} T_1 = 1000 {\rm \ kg\;} \times g \times { 1\over \sin(44^\circ) + \cos(44^\circ) \tan (56^\circ) } \label {eq:sln} \quad \end {equation}
$$ and T2 follows from $\eqref {eq:T2}$.

Done !

[edit] MathJax isn't being very cooperative -- things look OK from time to time but then they still appear in a framed box. Let me know and I'll TeX it a little less complicated...

 

[haruspex]

Hi Ted,
Might I ask what problem you are trying to solve? Are you having to determine counterweights or tension settings in order that the suspended load follows a particular trajectory? Or maybe you want to know the maximum horizontal load or torque at a pulley support?
If it's just the maximum tension on a cable, that's easy - that occurs when the load is directly beneath it.

 

[ted potts]

Hi, Thanks everyone for taking the time out to help me with this, however I'm still rather stuck, I think it may be the letters in the equation that are throwing me off, I have a casio fx-85gt plus calculator, could anyone write this out in single calculations? with the answers in kilograms? maybe then I can retrace the steps and understand the workings,

Thanks Ted

 

[Merlin3189]

If it's just the maximum tension on a cable, that's easy - that occurs when the load is directly beneath it.

So long as the angle between the chains stays less than about 90^o. (*)
The other factors that worry me are;
How much do the hoists need to be derated for a non-vertical load?
If the loads are such that calculations might be needed, should not this work be supervised by a suitably qualified and experienced engineer? Or at very least be strictly following a safe working plan drawn up by such an engineer?

Might it be worth moving this thread from Introductory Physics HW to a Mechanical Engineering forum, to perhaps attract the attention of a Mech.Eng. with knowledge of good practice in this area?

(*) My understanding of chain sling derating, is that upto 90^o is considered normal use without derating and 120^o is considered the maximum acceptable. It seems obvious that the tension would increase indefinitely if the included angle approached 180^o.

 

[ted potts]

Hi, yes that is correct, especially in a scenario where the anchor points are at equal heights and the load is in the middle horizontally, as a rule of thumb we say 90^ chain angle = 70% load on each anchor, and 120^ = 100% load on each anchor, however when anchors are at different heights the loads aren't symmetrical, and in the planning process we need to calculate these loads for every lift,, I will attach the method I currently use, but what I am looking for is the simplest way to calculate T1 and T2 in kgs using angles rather than lengths..Thanks Ted