yik-boh
- 57
- 0
Homework Statement
Find the volume of the described figures
1. A pyramid with height h and base an equilateral triangle with side a (a tetrahedron).
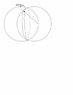
2. Find the volume common to two spheres each with radius r, if the center of each sphere lies on the surface of the other sphere.
These are hard problems and I really do not know what to do. Our teacher gave this to us as a challenge and I really would like to know how to solve these two. I hope you can help me by explaining each important step you will take. I hope you can make it detailed as much as possible. I really am having a hard time in Calculus. Thanks! :)