Finding volume/mass of 3D Solid

[dinospamoni]

Homework Statement

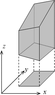
The volume shown lies above a square in the (x, y) plane having corners (4, 1), (5, 1), (5, 2), and (4, 2). The remaining two surfaces are planes defined by z1 = 2x + 4y + 7 and z2 = 3x + 6y + 8. The density of this object is 880.y. Determine a) the volume of this object, and b) the mass of this object.

A picture is attached

Homework Equations

I can't use the coding on here, so bear with me:

Volume of a 3D object is given by V=∫∫∫dxdydz

Mass of a 3D object is: m=∫∫∫ρdxdydx
where ρ is the density

The Attempt at a Solution

My setup for the volume is:

∫∫∫dzdxdy
Limits of integration:
2x+4y+7 < z < 3x + 6y + 8.
4<x<5
1<y<2

And for mass:

∫∫∫800y dzdxdy

with the same limits of integration

I've gotten 8.5 and 10333.3 for the volume and mass, respectively, but those are wrong.

Can anyone see what I'm doing wrong?

 

[LCKurtz]

Your work looks correct to me. I get the same answers as you.

 

[dinospamoni]

AH I see what I did wrong. When I calculated the mass I used density = 800y instead of 880y