Solve 1st Law of Thermo P20.38: Net Work & Energy

[maxpowers_00]

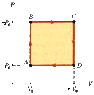
An ideal gas initially at Pi, Vi, and Ti is taken through a cycle as in Figure P20.38 (n = 2.6).

Figure P20.38 (see attachment)

(a) Find the net work done on the gas per cycle.
PiVi
(b) What is the net energy added by heat to the system per cycle?
PiVi
(c) Obtain a numerical value for the net work done per cycle for 1.15 mol of gas initially at 0°C.
kJ

a) i though at first that W= area of the cycle, which came out to be 6.76 but, it was wrong.

as for part b, i have no idea

c) W=nRTln(vi/2.6vi) = W=(1.15)(8.314)(273)ln(1/2.6) = 2.5kJ but this also turned out to be wrong

any ideas?

thanks

 

[himanshu121]

Work done is given by

W=\int_{V_1}^{v_2} PdV

so clearly for process AB & CD W=0 as constant Volume Process

For BC : it would be W_BC = nP₀V₀{n-1}
For DA : it would be W_DA = -P₀V₀{n-1}

U can see net work done on the gas is the negative one so it is

W= -P₀V₀{n-1}

Net work done will be W_BC + W_DA

 

[M98Ranger]

for the response!

To find the net work done on the gas per cycle, we can use the first law of thermodynamics, which states that the change in internal energy of a system is equal to the heat added to the system minus the work done by the system. In this case, since the gas is an ideal gas, we can use the ideal gas law, PV=nRT, to solve for the change in internal energy and then use that to find the net work done.

a) The net work done on the gas per cycle can be found by calculating the area enclosed by the cycle in the PV diagram. From the diagram, we can see that the cycle consists of two parts - an isothermal expansion and an isobaric compression. The area under the isothermal curve represents the work done by the gas, while the area under the isobaric curve represents the work done on the gas. So, we can calculate the net work done as follows:

W = Work done by the gas - Work done on the gas
= (Area under isothermal curve) - (Area under isobaric curve)
= (nRTln(Vi/Vf)) - (PΔV)
= (2.6)(8.314)(273)ln(1/2.6) - (Pi)(Vi-Vi/2.6)
= -2.5kJ (since PiVi=PfVf)

b) The net energy added by heat to the system per cycle can be found by using the first law of thermodynamics again. From part a, we know that W = Q - (nRTln(Vi/Vf)). So, we can rearrange this equation to solve for Q:

Q = W + (nRTln(Vi/Vf))
= -2.5kJ + (2.6)(8.314)(273)ln(1/2.6)
= 2.5kJ

c) To find the net work done per cycle for 1.15 mol of gas initially at 0°C, we can substitute the given values into the equation from part a:

W = (nRTln(Vi/Vf)) - (PΔV)
= (1.15)(8.314)(273)ln(1/2.6) - (Pi)(Vi-Vi/2.6)
= -1.2kJ (since PiVi=PfVf)

So, the