Fluid velocity (Bernoulli's Principle?)

[lifeiseasy]

Homework Statement

A wide tank contains a non-viscous liquid. The surface of the liquid is at a height 0.5 m above a hole situated at the bottom of the tank. Assuming streamline flow, calculate the velocity of the liquid emerging from the hole.

Homework Equations

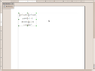
P + 1/2 Dv^2 + Dgh = constant (?)

The Attempt at a Solution

h=0.5 m
non-viscous -> density unchanged
Then? I can't continue.

 

[AtticusFinch]

Write out the constant side of Bernoulli's equation. It will describe the state of the water at the hole.

Hint: Since the water coming out the hole is coming into air the pressure on the water will also be atmospheric pressure (so it cancels from both sides).

 

[Phrak]

"non-viscous -> density unchanged"

Non-viscous means moving without frictional energy loss. When the densy is unchanged, it is incompressible. In this problem you assume incompressible as well as non viscous.

 

[lifeiseasy]

Thanks AtticusFinch for your hints and Phrak for your correction (I just mixed them up). I think I've arrived at the answer.

Is it correct?

 

[AtticusFinch]

Thanks AtticusFinch for your hints and Phrak for your correction (I just mixed them up). I think I've arrived at the answer.

Is it correct?

Yeah that looks correct to me. However you final units should be m/s