EngrDelaCruz
- 3
- 0
FLUIDS: Potential Flow Question -- URGENT HELP NEEDED
I need to submit this soon and I am way behind in this topic. I would appreciate it a lot if you can help me out figure the answer.
In a uniform onset flow of 7 m/s parallel with the x axis, a source of strength 19 m2/s per metre is located at the origin (x=0, y=0) and a sink of equal strength is located at (x=2, y=0). Locate the x-axis position of the most upstream stagnation point.
Diagram:
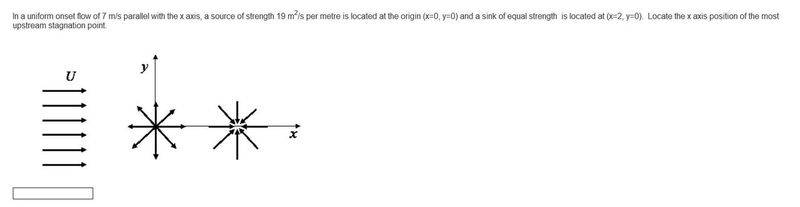
I think it will be these:
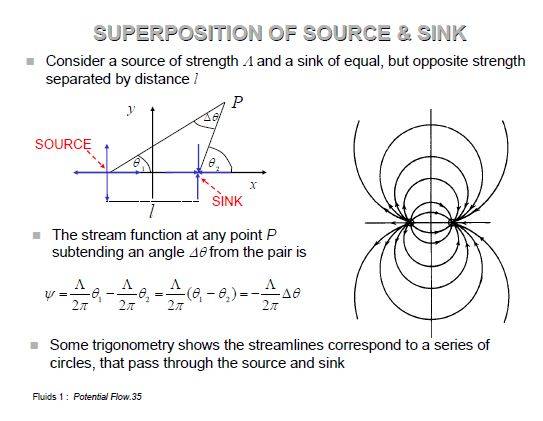

Figuring out the stream function:
Psi = (lambda / 2pi)(theta_1 - theta_2)
...
v=7m/s
...

Ugh.. please just help me out on this. It's 5% of the unit. Thanks
I need to submit this soon and I am way behind in this topic. I would appreciate it a lot if you can help me out figure the answer.
Homework Statement
In a uniform onset flow of 7 m/s parallel with the x axis, a source of strength 19 m2/s per metre is located at the origin (x=0, y=0) and a sink of equal strength is located at (x=2, y=0). Locate the x-axis position of the most upstream stagnation point.
Diagram:
Homework Equations
I think it will be these:
The Attempt at a Solution
Figuring out the stream function:
Psi = (lambda / 2pi)(theta_1 - theta_2)
...
v=7m/s
...
Ugh.. please just help me out on this. It's 5% of the unit. Thanks